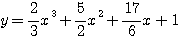
質問＜８９６＞２００２／７／２４
from=hajime
「数列の応用？」

x≧0 y≧0 z≧0 x+y+2z≦2n (nは0以上の整数）を満たす
x,y,zの組(x,y,z)の個数。

xとyだけなら何とか分かるんですがzが入ってくるとわけが
わかりません。おねがいします。

お返事２００２／７／２４
from=武田

ｎが変化するにしたがって個数が変わるから、数列の問題ですね。
ｎ＝０から１つずつ増やしながら、個数を数えていきます。
ｎ＝０のとき、
　　（ｘ，ｙ，ｚ）＝（０，０，０）　１個
ｎ＝１のとき、
　　（ｘ，ｙ，ｚ）＝（０，０，０）
　　　　　　　　　　（０，０，１）
　　　　　　　　　　（０，１，０）
　　　　　　　　　　（１，０，０）
　　　　　　　　　　（１，１，０）
　　　　　　　　　　（２，０，０）
　　　　　　　　　　（０，２，０）　７個
しかしながら、どうにも面倒なので、
十進Ｂａｓｉｃでプログラムして、
--------------------------------------
for n=0 to 10 step 1
   let  count=0
   for x=0 to 100 step 1
      for y=0 to 100 step 1
         for z=0 to 100 step 1
            if x+y+2*z＜=2*n then 
               let  count=count+1
            else
            end if
         next z
      next y
   next x
   print n;count
next n
end
--------------------------------------
　ｎ　　count
　０　　１
　１　　７
　２　　２２
　３　　５０
　４　　９５
　５　　１６１
　６　　２５２
　７　　３７２
　８　　５２５
　９　　７１５
１０　　９４６

この数列の一般項を出すのは難しいので、
私の得意な「幻の０番法」で解きました。

階差を取ると、第３階差で一定の４となるので、元の数列は３次関数と
なるから、
３次関数ｙ＝ａｘ3 ＋ｂｘ2 ＋ｃｘ＋ｄのときの公式より、
｛　　　　ｄ＝１
｛ａ＋ｂ＋ｃ＝６
｛６ａ＋２ｂ＝９
｛　　　６ａ＝４
これを解くと、
｛ａ＝２／３
｛ｂ＝５／２
｛ｃ＝１７／６
｛ｄ＝１
したがって、

したがって、

 ………（答）

ようやく休みになりましたが，いかがでしょうか？
ｄ３です．よろしくお願いします．

質問＜８９６＞２００２／７／２４「数列の応用？」
この問題，私も解答してみました．
x≧0，y≧0，z≧0で，x＋y＋2z≦2n (nは0以上の整数）の
(x，y，z)の組（正の整数解）を考えることは，
w＝2n－(x＋y＋2z)として考えると，w≧0で，
x＋y＋2z＋w＝2n (nは0以上の整数）の
(x，y，z，w)の組（正の整数解）を考えることと本質的に
同じコトです．
さらにzを固定して考えると，
x＋y＋w＝2(n－z) (nは0以上の整数）の
(x，y，w)の組（正の整数解）を考えて，
2(n－z)＝0，2，・・・，2nの場合で，その組の個数を
すべて加えればいいのです．
x＋y＋w＝2(n－z) (nは0以上の整数）の
(x，y，w)の組（正の整数解）の個数は，
n－z＝k－1として，
C(2k，2)＝(2k)(2k－1)/2＝k(2k－1)です．
（組合せのnＣrをC(n，r)とかいています．）
　C(2，2)＋C(4，2)＋C(6，2)＋・・・＋C(2n＋2，2)
＝∑(k＝1→n＋1)，k(2k－1)
これで答えが出てきます．
（最後のところを二項定理でやるのもあるかな？）

お身体をくれぐれもご自愛ください．
またおじゃまします．（毎日おじゃましています）．
それでは，失礼します．