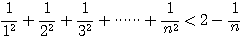





質問<808>2002/3/18
from=もんもん
「数学的帰納法について」
はじめまして。突然なんですが解答を見ても下記に記した変形方法が
わかりません。教えてください。
1/1^2+1/2^2+1/3^2+・・・・+1/n^2<2-1/n (n は2以上)
を帰納法で証明せよ
という問題です
<証明>
n=2のとき5/4<3/2となり成立
n=kのとき 1/1^2+1/2^2+1/3^2+・・・・+1/k^2<2 - 1/k
と
が成立すると仮定
n=k+1のとき両辺に1/(k+1)^2を加えると
1/1^2+1/2^2+1/3^2+・・・・+1/k^2+1/(k+1)^2<2- 1/k + 1/(k+1)^2
(右辺)=2- 1/k + 1/(k+1)^2
↓ この部分の変形方法が
=2- 1/k + 1/k(k+1) 分かりません
=2 -1/k+1
お返事2002/3/19
from=武田
が、nは2以上のとき、成り立つことを数学的帰納法で証明すると、
(1)n=2のとき、
左辺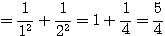
右辺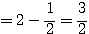
したがって、左辺<右辺
(2)n=kのとき成り立つと仮定して、
n=k+1のとき、
左辺
右辺
したがって、左辺<右辺
nが2以上の自然数のとき、与式は成り立つ。
証明終了




