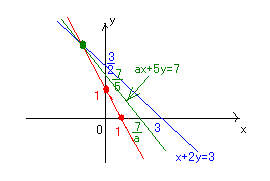
質問＜７２２＞２００１／１２／７
from=ゆうき
「直線の応用」

①２直線ｘ＋2ｙ＝3，ａｘ＋5ｙ＝7の交点を通る直線が
2点（1,0）、（0,1）を通るとき、ａの値を求めよ。

②点（－1,3）を通り、互いに直交する2本の直線があって、
それらは原点からの距離が等しいという。
この2本の直線の方程式を求めよ。

お返事２００１／１２／２０
from=武田

問１

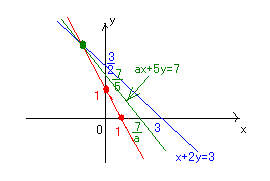
｛ｘ＋２ｙ＝３

｛ａｘ＋５ｙ＝７

連立して、

（２ａ－５）ｙ＝３ａ－７

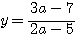
したがって、

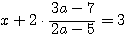
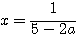
２直線の交点の座標は、

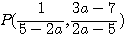
２点（１，０）、（０，１）を通る直線は、ｘ＋ｙ＝１より、代入して、

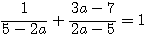
∴ａ＝３………（答）

問２

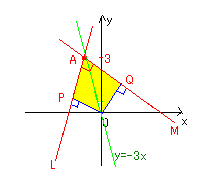
原点Ｏから、問題の２直線Ｌ、Ｍに垂直な直線を下ろした足をＰ、Ｑとする。

Ｌの傾きをａとすると、ｙ－３＝ａ（ｘ＋１）より、

　　　　　　　　　　　　ｙ－ａｘ－（ａ＋３）＝０

原点からの距離は、公式より、

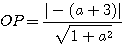
同様にして、

Ｍの傾きをｂとすると、

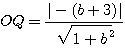
ＯＰ＝ＯＱより、

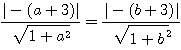
直線ＬとＭは垂直だから、ａ×ｂ＝－１

上の計算をすると、

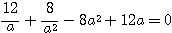
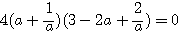
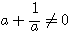より、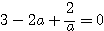

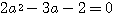
（２ａ＋１）（ａ－２）＝０

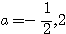
したがって、

２直線Ｌ、Ｍの方程式は、

｛ｙ＝２ｘ＋５

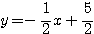｛  ………（答）