質問＜３５４２＞２００７／５／１５
from=JUN*2
「確率」

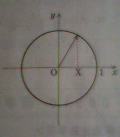
次の問題についてお伺いします。
図のようにルーレットの棒の先をx軸におろした足のx座標をXとする。
次の問いに答えよ。ただし、ルーレットの半径は1とする。
1.Y=|X|とするとき、Yの分布関数F_Y(y)を求めよ。
2.Yの確率密度関数p_Y(y)を求めよ。



★希望★完全解答★

お便り２００７／５／１６
from=juin

円周上での針先がとまる位置はどこをとっても同じ確率と仮定する。
P(Y＜y)
=P(|X|＜y)
=P(-y＜X＜y)
=P(-y＜cost＜y)
=2P(-y＜cost＜y,0＜t＜π)
=4P(0＜cost＜y,0＜t＜π/2)
=4P(Arccosy＜t＜π/2)
=4{(π/2)-Arccosy}/(2π)
=1-(2/π)Arccosy
dP/dy=-2/(π√(1-y^2))