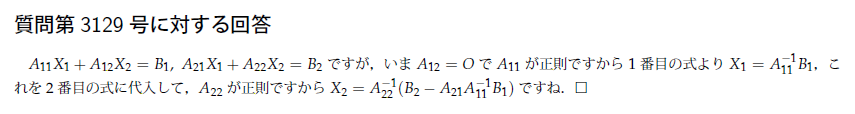
質問＜３１２９＞２００６／４／２８
from=チャッピー
「行列の問題」

n,n1,n2,Lを自然数とし、n1+n2=nである。行列Aはｎ次正方行列、行列Bはｎ×L行列
である。A=A（k,L),A(k,L)はn(k)行n(L)列(1≦k,L≦2)であり、
B=B(i),B(i)はn(i)行L列（i=1,2)と言うようにAとBをそれぞれ分割する。
A（1,2)=0かつA(1,1)とA(2,2)がともに正則であるとする。
このときAX=Bを満たすn行ｎ列の行列Xが一意的に存在する。
このことをX=X(i)、X(i)はn(i)行L列と分割して
A(1,1)X(1)+A(1,2)X(2)=B(1),A(2,1)X(1)+A(22)X(2)=B(2)⇔X(1)=C(1),X(2)=C(2)
という同値を導くことによって示せ。
またC(i)はn(i)行L列の行列（i=1,2)であるとする。
という問題です。よろしくお願いします。

★希望★完全解答★

お便り２００７／６／８
from=cqzypx