質問＜２６２＞２０００／５／２６
from=陽子
「関数」

《１》aは実数の定数とする。
2次方程式 Ｘ[二乗]+2aＸ+（2a[二乗]-2/3a-1/3）=0が実数解α、βを
もつとき、α+βの値の範囲と、αβの値の範囲を求めよ。

《２》2次方程式 X[二乗]-3Ｘ+1=0の2解をα、βとする。
F（α）=kβ、F（β）=kα、F（1）=kを満たす2次式 F（Ｘ）をkを用い
て表せ。ただしk≠0とする。

お返事２０００／５／２７
from=武田

問１
　　　　　　　　　　　　２　　１
ｘ2 ＋２ａｘ＋（２ａ2 －─ａ－─　）＝０
　　　　　　　　　　　　３　　３
が実数解をもつには、判別式Ｄ／４≧０より、
　　　　　　　　２　　１
ａ2 －（２ａ2 －─ａ－─　）≧０
　　　　　　　　３　　３
３ａ2 －２ａ－１≦０
（３ａ＋１）（ａ－１）≦０
　　１
∴－─≦ａ≦１　……①
　　３
また、解と係数の関係より、
｛α＋β＝－２ａ
｛　　　　　　　２　　１
｛αβ＝２ａ2 －─ａ－─
｛　　　　　　　３　　３
α＋βの値の範囲は①より、
　　　　　　　２
－２≦α＋β≦─　……（答）
　　　　　　　３
αβの値の範囲は、平方完成して、
　　　　　　　２　　１　　　　　　１　　　　１
αβ＝２ａ2 －─ａ－─＝２（ａ2 －─ａ　）－─
　　　　　　　３　　３　　　　　　３　　　　３

　　　　　　１　　　１　　１　　　１
＝２（ａ2 －─ａ＋──－──　）－─
　　　　　　３　　３６　３６　　　３

　　　　　１　　　　　１　１
＝２（ａ－─　）2 －──－─
　　　　　６　　　　１８　３

　　　　　１　　　　　７
＝２（ａ－─　）2 －──
　　　　　６　　　　１８
①の範囲を定義域にして、値域を求めると、

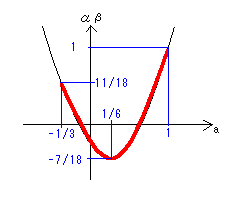　　７
－──≦αβ≦１　……（答）
　１８

問２
ｘ2 －３ｘ＋１＝０は判別式Ｄ＝９－４＝５＞０より、
２つの異なる実数解をもつので、それをαとβとすると、解と係数の関係より、
α＋β＝３、αβ＝１　……①
２次式Ｆ（ｘ）＝ａｘ2 ＋ｂｘ＋ｃとおくと、条件より、
Ｆ（α）＝ａα2 ＋ｂα＋ｃ＝ｋβ……②
Ｆ（β）＝ａβ2 ＋ｂβ＋ｃ＝ｋα……③
Ｆ（１）＝ａ＋ｂ＋ｃ＝ｋ……④
②＋③より、
ａ（α2 ＋β2 ）＋ｂ（α＋β）＋２ｃ＝ｋ（β＋α）
①より、α2 ＋β2 ＝（α＋β）2 －２αβ
＝３2 －２×１＝９－２＝７
７ａ＋３ｂ＋２ｃ＝３ｋ……⑤
②－③より、
ａ（α2 －β2 ）＋ｂ（α－β）＝ｋ（β－α）
ａ（α－β）（α＋β）＋ｂ（α－β）－ｋ（β－α）＝０
（α－β）｛ａ（α＋β）＋ｂ＋ｋ｝＝０
α≠βより、α－β≠０
したがって、ａ（α＋β）＋ｂ＋ｋ＝０
３ａ＋ｂ＋ｋ＝０……⑥
④⑤⑥を連立して、
｛ａ＋ｂ＋ｃ＝ｋ……④
｛７ａ＋３ｂ＋２ｃ＝３ｋ……⑤
｛３ａ＋ｂ＋ｋ＝０……⑥
④×２－⑤より、
　　２ａ＋２ｂ＋２ｃ＝２ｋ
－）７ａ＋３ｂ＋２ｃ＝３ｋ
　────────────
　　－５ａ－ｂ　　　＝－ｋ
　　５ａ＋ｂ－ｋ＝０……⑦
⑥－⑦より、
　　３ａ＋ｂ＋ｋ＝０
－）５ａ＋ｂ－ｋ＝０
　─────────
　　－２ａ　＋２ｋ＝０
　　∴ａ＝ｋ
⑥に代入して、
３ｋ＋ｂ＋ｋ＝０
　　∴ｂ＝－４ｋ
④に代入して、
ｋ＋（－４ｋ）＋ｃ＝ｋ
　　∴ｃ＝４ｋ
したがって、
Ｆ（ｘ）＝ｋｘ2 －４ｋｘ＋４ｋ＝ｋ（ｘ2 －４ｘ＋４）
　　　　＝ｋ（ｘ－２）2 ……（答）