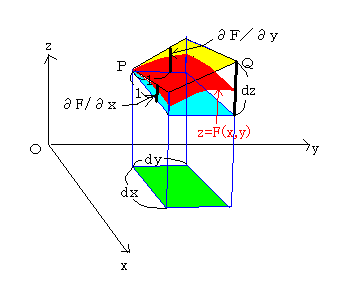
 二変数関数z=F(x、y)の全微分は、必ず
∂F ∂F
dz=──dx+──dy
∂x ∂y
となる。
この∂F/∂xと∂F/∂yの比が一定(a/b)という
条件のもとで、解答を求めると、(微分方程式の解は関数
となる)
dz=adx+bdy
積分して、
z=ax+by……(答)
両方を代入して計算したが、片一方だけ代入というほうの
解は不明。誰かアドバイスを!
二変数関数z=F(x、y)の全微分は、必ず
∂F ∂F
dz=──dx+──dy
∂x ∂y
となる。
この∂F/∂xと∂F/∂yの比が一定(a/b)という
条件のもとで、解答を求めると、(微分方程式の解は関数
となる)
dz=adx+bdy
積分して、
z=ax+by……(答)
両方を代入して計算したが、片一方だけ代入というほうの
解は不明。誰かアドバイスを!





質問<201>99/12/17
x、y、zの3次元の図で、z=F(x、y)としたとき、
dF(x、y)={[∂F(x、y)/∂x]・dx}+{[∂F(x、y)/∂y]・dy}
を(1)式とします。
他方、[∂F(x、y)/∂x]/[∂F(x、y)/∂y]=a/b
(a、bは定数) を(2)式とします。
ここでご教授いただきたいのですが、
(1)式においても、(2)式を成立させるには、つまり(1)式と
(2)式を連立して解くには、(1)式の[∂F(x、y)/∂x]に、
(2)式を変形した[∂F(x、y)/∂x]=[a/b]・[∂F(x、y)/∂y]
を代入するか、または、(1)式の[∂F(x、y)/∂y]に、(2)式
を変形した[∂F(x、y)/∂y]=[b/a]・[∂F(x、y)/∂x]を
代入するかすればよいわけですが、なぜ、どちらか一方に(2)
式の変形を代入すれば、(1)式においても(2)式を考慮したこ
とになるのでしょうか?
また、どちらか一方でなく、上記の両方に(2)式の変形を代入
してもよいそうですが、これはなぜなのでしょうか?
確かに、たとえばy=x+2と、y=3x+4という2変数の連立の
場合、y=x+2のyに3x+4を代入して解くというのは自然に
行ってきたことなので、特に疑問を持ったことはなかったの
ですが。
お返事99/12/21
from=武田
二変数関数z=F(x、y)の全微分は、必ず ∂F ∂F dz=──dx+──dy ∂x ∂y となる。 この∂F/∂xと∂F/∂yの比が一定(a/b)という 条件のもとで、解答を求めると、(微分方程式の解は関数 となる) dz=adx+bdy 積分して、 z=ax+by……(答) 両方を代入して計算したが、片一方だけ代入というほうの 解は不明。誰かアドバイスを!




