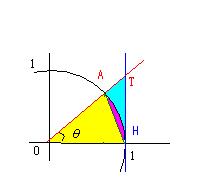
 0<θ<π/2(ラジアン)で、面積を考える。
△OAH=sinθ・1÷2
扇形OAH=1^2・θ÷2
△OTH=tanθ・1÷2
△OAH<扇形OAH<△OTH
sinθ<θ<tanθ
sinθで割ると、
θ 1
1<―――<―――
sinθ cosθ
逆数を考えて、
sinθ
1>―――>cosθ
θ
lim cosθ=1より、
θ→0
sinθ
lim ―――=1
θ→0 θ
0<θ<π/2(ラジアン)で、面積を考える。
△OAH=sinθ・1÷2
扇形OAH=1^2・θ÷2
△OTH=tanθ・1÷2
△OAH<扇形OAH<△OTH
sinθ<θ<tanθ
sinθで割ると、
θ 1
1<―――<―――
sinθ cosθ
逆数を考えて、
sinθ
1>―――>cosθ
θ
lim cosθ=1より、
θ→0
sinθ
lim ―――=1
θ→0 θ





質問<1422>2003/9/27
いつもお世話になっております。
先日の不等式については、アドバイス頂き有難う御座いました。
今回も初歩的なことで恐縮ですが、よろしくお願い致します。
(sin x)' = cos x の証明について
(sin x)' = lim { ( sin(x+h) - sin x ) / h }
h→0
和積公式より
= lim 1/h { 2 cos( x + h/2 ) sin h/2 } ...(1)
h→0
この後から進められなくなり、参考書を調べていると
lim sinθ / θ = 1 ...(2)
θ→0
という式を見つけ、
lim cos( x + h/2 ) sin( h/2 ) / 2/h = cos x
h→0
と証明することができました。
が、(2)の式については、漠然とそう記載されているだけで
私には何故そうなるのかが理解できません。
よろしくお願い致します。
お返事2003/9/27
from=武田
0<θ<π/2(ラジアン)で、面積を考える。 △OAH=sinθ・1÷2 扇形OAH=1^2・θ÷2 △OTH=tanθ・1÷2 △OAH<扇形OAH<△OTH sinθ<θ<tanθ sinθで割ると、 θ 1 1<―――<――― sinθ cosθ 逆数を考えて、 sinθ 1>―――>cosθ θ lim cosθ=1より、 θ→0 sinθ lim ―――=1 θ→0 θ




