質問＜８５＞９８／１１／２１
from=水島愛
「いろいろな問題」

（問１）１辺の長さが２aの正三角形ＡＢＣにおいて、辺ＡＣ
の中点をＤ、線分ＢＤの中点をＥとし、∠ＥＣＢ=∂とすると
き、次の問に答えなさい。

（１）線分ＥＣの長さをａを用いて表しなさい。

（２）ｓｉｎ∂の値を求めなさい。

（問２）２つの直線　３ｘ＋２ｙ＋３＝０と２ｘ－ｙ＋ｋ＝０
が、第３象限（ｘ＜０，ｙ＜０）において、交点を持つとき、
ｋの値を求めなさい。

（問３）下の連立の示す領域を図示して、その領域の面積を
求めなさい。

　Ｘ2＋Ｙ2－４≦０……①
　Ｙ－Ｘ－２≧０………………②
　Ｙ－Ｘ＋２≦０………………③
　Ｙ＋Ｘ－２≧０………………④
　Ｙ＋Ｘ＋２≦０………………⑤

（問４）ｓｉｎ（ｘ－π／６）＋ｃｏｓ（x－π／３）という
式の答えは？？

お返事９８／１１／２１
from=武田

（問１）

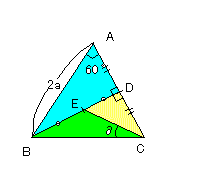（１）△ＥＣＤにおいて
ＣＤ＝ａ、ＥＤ＝ＢＤ／２＝(√３ａ)／２＝√３／２・ａより
三平方の定理より
ＥＣ2＝ＣＤ2＋ＥＤ2
　　　＝ａ2＋(√3/2・ａ)2
　　　＝7/4・ａ2
∴ＥＣ＝√７／２・ａ……（答）

（２）ｓｉｎ∂の値を求めなさい。
∠ＥＣＤ＝θとおくと、
　　　　ＥＤ　　√3/2ａ　　√21
sinθ＝───＝────＝────　……①
　　　　ＥＣ　　√7/2ａ　　　７
　　　　ＣＤ　　　ａ　　　２√7
cosθ＝───＝────＝────　……②
　　　　ＥＣ　　√7/2ａ　　　７
∠ＢＣＤ＝６０°より
sin∂＝sin(６０°－θ)
加法定理より
sin(６０°－θ)＝sin６０°cosθ－cos６０°sinθ
　　　　　　　＝√3/2cosθ－1/2sinθ
①②より
sin∂＝√3/2・２√7/7－1/2・√21/7
　　＝√21/7－√21/14
　　＝√21/14……（答）

（問２）
連立して
　３ｘ＋２ｙ＋３＝０……①
　２ｘ－ｙ＋ｋ＝０………②
②を変形して、ｙ＝２ｘ＋ｋを①に代入すると、
３ｘ＋２(２ｘ＋ｋ)＋３＝０
３ｘ＋４ｘ＋２ｋ＋３＝０
７ｘ＋２ｋ＋３＝０
　　－２ｋ－３
ｘ＝──────　……③
　　　　７
③を②に代入して、
　　－４ｋ－６　　　　３ｋ－６
ｙ＝──────＋ｋ＝─────　……④
　　　　７　　　　　　　　７
③④は第３象限（ｘ＜０，ｙ＜０）より
③より
－２ｋ－３＜０
２ｋ＞－３
ｋ＞－3/2　……⑤
④より
３ｋ－６＜０
３ｋ＜６
ｋ＜２　……⑥
⑤と⑥より
∴－3/2＜ｋ＜２……（答）

（問３）
　Ｘ2＋Ｙ2≦４……①
と下の領域１つ１つと連立して
　Ｙ≧Ｘ＋２…………………②
　Ｙ≦Ｘ－２…………………③
　Ｙ≧－Ｘ＋２………………④
　Ｙ≦－Ｘ－２………………⑤

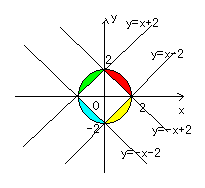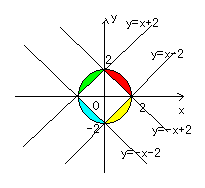重なった面積の和は、半径２の円から正方形を引いたところ
になるので、Ｓ＝π２2－(２√２)2
　＝４π－８……（答）

（問４）
加法定理
sin(α－β)＝sinαcosβ－cosαsinβ
cos(α－β)＝cosαcosβ＋sinαsinβ
より、
sin(ｘ－π／６)＋cos(ｘ－π／３)
＝sinｘ・cos(π／６)－cosｘ・sin(π／６)
＋cosｘ・cos(π／３)＋sinｘ・sin(π／３)
＝√３/2・sinｘ－1/2・cosｘ＋1/2・cosｘ＋√３/2・sinｘ
＝√３・sinｘ……（答）
これは変形するという問題ですね。