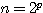質問＜７７１＞２００２／１／２０
from=戒兎
「相加相乗平均の一般化の証明」

nが自然数であるとき、
（a1>0）∧(a2>0)∧・…∧(an>0)
⇒(a1+a2+…+an)/n≧(a1×a2×・…×an)の1/n乗
を証明せよ。

等号成立⇔a1=a2=・…=an

お便り２００２／１／２２
from=ｄ３

質問＜７７１＞の解答です．
こんなのもいいのでは？
a＞0，b＞0で，次は既知とします．
(a＋b)/2≧√(ab)  ・・・＃
pを自然数とするとき，q＝2^pで，
a［1］，a[2]，a[3]，・・・,a[q]  で，ふたつずつで＃に当てはめる．
(a[1]＋a[2])/2≧√(a[1]a[2]) ，
(a[3]＋a[4])/2≧√(a[3]a[4]) ，
・・・・・・
(a[q－1]＋a[q])/2≧√(a[q－1]a[q]) ．
出てきた不等式で右辺をまた，ふたつずつ＃に当てはめる．
これを繰り返すと，
(a[1]＋・・・＋a[q])/q≧(a[1]×・・・×a[q])^(1/q) ・・・％
そして，ここで等号が成り立つのはすべてのa[j]が等しいときです．
n＝２の累乗のときは証明できたので，
いま，2^(p－1)＜n＜2^p＝q　とします．
m＝(a[1]＋・・・＋a[n])/nとかきます．
さらに，a[n＋1]＝a[n＋2]＝・・・＝a[q]＝mとすると，
a[1]＋・・・＋a[n]＝mn，a[n＋1]×・・・×a[q]＝m^(q－n) で，
％から，
｛mn＋(q－n)m)/q≧｛a[1]×・・・×a[n]×m^(q－n)｝^(1/q)
m≧｛a[1]×・・・×a[n]×m^(q－n)｝^(1/q)
両辺をq乗して，m^q≧a[1]×・・・×a[n]×m^(q－n)
よって，m^n≧a[1]×・・・×a[n]
これの両辺のn乗根をとれば，問題の不等式は証明されたことになります．

お便り２００２／２／９
from=ＧＯ

771の他の方法とかわないのでしょうか？

お返事２００２／２／９
from=武田

ｄ３さんが証明したのが、一般化の証明法ですので、
他には無いと思われます。

お便り２００２／２／１０
from=ＧＯ

すみませんがｍのていぎがよくわからないのですが？

お返事２００２／２／１１
from=武田

ｄ３さんの証明を分かりやすく表現してみると、

①ｎが２の累乗のとき、 とすると、

　 ………（＃）を既知として、

　の左辺を（＃）を利用して、

 これを２つずつ繰り返して、

②ｎが２の累乗以外のとき、 とすると、

　 とすると、 とおいて、

　（ｑ－ｎ）個の すべてを上のｍとおくと、

　①より、

 したがって、

　両辺をｑ乗して、

  したがって、ｎ乗根をとると、

①②より、すべての整数ｎ≧２で、相加平均相乗平均の一般化は証明できた。

武田  様

長男の受験勉強の手助けをしていて、標記の問題を解説した後、
たまたま「高校数学の窓」に遭遇し、楽しませていただきました。

それで、

> ｄ３さんが証明したのが、一般化の証明法ですので、
> 他には無いと思われます。
に関して、ちょっと気にかかり、お便りさせていただきます。

要点は、次の通りです。

1) 相加平均と相乗平均の関係は、対数関数を通して見た方が
   見通しがよい。

2) すなわち、相乗平均とは、対数をとって平均することである
   と思う。そう思えば、相乗平均では、相当大きい数でも小さく
   評価されて平均されるので、平均値が小さめになることは、
   直感的にも理解しやすい。

3) こういう感覚での証明の要点は次の通り。
 
   ① 対数関数が上に凸であることから

        ===> f(s*a + t*b) >= s*f(a) + t*f(b)
                ここで、s, t >=0; s+t=1

        ===> 上の性質を使って、数学的帰納法により、一般に
            f((a+b+...)/n) >= (1/n)*(f(a)+f(b)+...)
            を示す。

   ② 対数関数が単調増加であることから、大小関係が
        値域と定義域で同じ方向に保たれる。

すなわち、相加・相乗平均の関係は、対数関数の凸性と単調性
からの単純な帰結であるということです。
ご存じかもしれませんが、念のためお知らせしました。

----
数学が苦手の受験生の父より

「相加・相乗平均の一般化の別証明」につき、
ページへの掲載、ありがとうございました。

そのまま掲載されることを意図しなかったため、高校生向けという
意味では説明不足の懸念があり、要点のみで恐縮ですが、補足
いたします。

問題は、対数関数が上に凸であることから、

    (1)    f(s*a + t*b) >= s*f(a) + t*f(b)
                ここで、s, t >=0; s+t=1

と簡単に片付けてしまっていることにあります。
(1) は、むしろ、凸であることの定義であり、より正確には、例えば

    (2)    区間[a, b] で関数 f が上に凸であること

            ＜＝＞（定義）

            任意の x1, x2 ∈ [a,b] に対して

            f(s*x1+ t*x2) >= s*f(x1) + t*f(x2)

            ここで、s,t は s, t >=0; s+t=1 を満たす任意の実数。

というように定義します。不等式の右辺は、関数のグラフで、x1, x2
に対応する関数値を表す２点を結ぶ線分を任意の比率で内分した
点の高さを示しますので、不等号は、その点で関数値が上にある
ことを示します。

このように定義した上で、これが微分可能な関数の場合には、

    (3)    区間[a,b] で２階微分可能な関数が上に凸

            ＜＝＞ ２階導関数がその区間で正の値をとらない

ということが平均値の定理を使って証明できます。

対数関数の２階導関数は -1/x^2 で正値をとらないので (3) に該当
するというわけです。

なお、対数関数を使うということは、指数の概念をｎ乗・ｎ乗根（1/n乗）
という自然数から、実数にまで拡張した段階での話であり、そういう
視点から見ると、相加相乗平均の大小関係が、凸というより一般的な
性質から、１つの必要条件として出てくるということです。

すなわち、この証明方法は、上記のような解析学の基礎的な知識を
前提にして成り立つものですので、その辺りの話を抜きにして

    「単純な帰結」

と言ってしまっては、証明の肝心な部分を省略して、単純に見える
という印象を与えたに過ぎなかったかなと反省しています。

前提知識が少なくてすむという意味で、高校生向けには、ｄ３さん式
の証明が無難かもしれませんが、より一般的な視点から問題を
見ておく意味はあるのではないかと思います。

----
数学では目標を達成しても、物理で失敗した受験生の父