




質問<753>2001/12/30
from=Syun
「∑計算の法則」
∑計算の練習やってるうちに、このような法則があるのではないかと思 ったのですが、真偽を証明することはできるでしょうか。 n m+p n+p+1 ∑ (Πk)= Π k /p+2 (pは0以上の定数) m=1 k=m k=n
お便り2002/1/5
from=d3
質問<753>の解答です.
>pは0以上の定数
これは自然数ということですね.
Σはfrom m=1 to n とします.
∑m(m+1)(m+2)・・・(m+p)=n(n+1)(n+2)・・・(n+p+1)/(p+2)
を示せばいいのですね.
証明はじめ>>
m(m+1)(m+2)・・・(m+p)
={m(m+1)(m+2)・・・(m+p)}×[{(m+p+1)-(m-1)}/(p+2)]
((∵)うしろの[]の中は1です!)
=[{m(m+1)(m+2)・・・(m+p)(m+p+1)}
-{(m-1)m(m+1)(m+2)・・・(m+p)}]/(p+2)
ここで,A[n]=n(n+1)(n+2)・・・(n+p+1) とすると,
m(m+1)(m+2)・・・(m+p)
={A[m]-A[m-1]}/(p+2)
したがって,証明すべき式の左辺を(p+2)倍しておくと,
(p+2)×∑m(m+1)(m+2)・・・(m+p)
=(A[1]-A[0])+(A[2]-A[1])+(A[3]-A[2])+・・・
+(A[n]-A[n-1])
=A[n]
((∵)A[0]=0 )
よって,問題の式は証明されました.
お返事2002/1/5
from=武田
d3さんの証明は見事ですね。 私は「差分・和分」の本を読んでみました。 計算ができましたので、参考までお知らせします。 前提として、次の3つを紹介します。 ①階乗関数として、
②和分の公式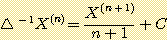
③定和分の公式
与式の左辺=
(∵
より)
=右辺




