




質問<625>2001/8/29
from=えび
「直線の方程式の決定」
はじめまして。文系の高2生です。
問. 2本の直線 3x+4y-11=0・・・・・・①,
12x-5y-2=0・・・・・・② の交点をPとする。
(1)原点(0,0)と点Pを通る直線の方程式は y=ァ( )である。
(2)点Pを通り、直線①に垂直な直線の方程式は y=ィ( )である。
(3)点Pを通る直線l (←小文字のエル)が円x^2+y^2=2によって切り取
られる線分の長さが2のとき、直線lの方程式は y=ゥ( )で
ある。ただし、l の傾きは正とする。
・(1)と(2)の答えは分かった(ァ→y=2x,ィ→y=-1/2)のですが、
(3)の途中式が分かりません。
交点P(1,2)〔←先に求めたものと考えて。〕
(3) 傾きをm(m>0)とすると、点Pを通る直線 y=m(x-1)+2
ゆえに mx-y+2-m=0・・・・・・③
円 x^2+y^2の中心と直線 mx-y+2-m=0の距離d は,
d=[2-m]/√m^2+1
↑絶対値
題意を満たすとき、d^2+(2/2)^2=(√2)^2
ゆえに d^2=1
よって (2-m)^2=m^2+1 これを解いて m=3/4
求める直線の方程式は y=3/4x+5/4
と解答にも、答えられていました。
解答を見て考えても、青色の式は何の式なのかよく分かりません。
なので、赤色の部分もよく分かりません。
なぜ、こうなるのか教えてください!!!
お返事2001/8/31
from=武田
メールの関係で、色の部分が消えてしまいましたので、
どこがわからないかわかりませんが、推測して答えます。
(1)
連立を解いて、
{3x+4y-11=0………①
{12x-5y-2=0………②
①×4-②より、
21y-42=0
∴y=2
①に代入して
3x+8-11=0
∴x=1
交点Pの座標は(1,2)となる。
したがって、
y=2x………(答)
(2)
①の傾きは
4y=-3x+11
3 11
y=-―x+――
4 4
より、
3
m=-―
4
直交条件より、
m’×m=-1より、
3
m’×(-―)=-1
4
4
∴m’=―
3
点P(1,2)を通るから、
4
y-2=―(x-1)
3
4 4 4 2
y=―x-―+2=―x+―………(答)
3 3 3 3
(3)
点Pを通る傾きがmの直線の方程式は、
y-2=m(x-1)
y=mx-m+2
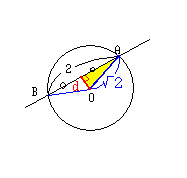 円x2 +y2 =2の中心(0,0)から切断した直線への
最短距離dは、
|
|<直線とその外の点からの距離の公式>
| 直線の方程式ax+by+c=0、外の点(α,β)のとき、
| |aα+bβ+c|
| d=―――――――――
| √(a2 +b2 )
|
直線の式を変形して、
mx-y-m+2=0より、
|m・0-0-m+2| |2-m|
d=―――――――――――=―――――――
√{m2 +(-1)2 } √(m2 +1)
図の△OAHは直角三角形だから、三平方の定理より、
d2 +12 =(√2)2
∴d2 =1
したがって、
(2-m)2
――――――=1
(m2 +1)
(2-m)2 =(m2 +1)
4-4m+m2 =m2 +1
4m=3
3
∴m=―
4
点P(1,2)を通るから
3
y-2=―(x-1)
4
3 3 3 5
y=―x-―+2=―x+―………(答)
4 4 4 4
円x2 +y2 =2の中心(0,0)から切断した直線への
最短距離dは、
|
|<直線とその外の点からの距離の公式>
| 直線の方程式ax+by+c=0、外の点(α,β)のとき、
| |aα+bβ+c|
| d=―――――――――
| √(a2 +b2 )
|
直線の式を変形して、
mx-y-m+2=0より、
|m・0-0-m+2| |2-m|
d=―――――――――――=―――――――
√{m2 +(-1)2 } √(m2 +1)
図の△OAHは直角三角形だから、三平方の定理より、
d2 +12 =(√2)2
∴d2 =1
したがって、
(2-m)2
――――――=1
(m2 +1)
(2-m)2 =(m2 +1)
4-4m+m2 =m2 +1
4m=3
3
∴m=―
4
点P(1,2)を通るから
3
y-2=―(x-1)
4
3 3 3 5
y=―x-―+2=―x+―………(答)
4 4 4 4





 円x2 +y2 =2の中心(0,0)から切断した直線への
最短距離dは、
|
|<直線とその外の点からの距離の公式>
| 直線の方程式ax+by+c=0、外の点(α,β)のとき、
| |aα+bβ+c|
| d=―――――――――
| √(a2 +b2 )
|
直線の式を変形して、
mx-y-m+2=0より、
|m・0-0-m+2| |2-m|
d=―――――――――――=―――――――
√{m2 +(-1)2 } √(m2 +1)
図の△OAHは直角三角形だから、三平方の定理より、
d2 +12 =(√2)2
∴d2 =1
したがって、
(2-m)2
――――――=1
(m2 +1)
(2-m)2 =(m2 +1)
4-4m+m2 =m2 +1
4m=3
3
∴m=―
4
点P(1,2)を通るから
3
y-2=―(x-1)
4
3 3 3 5
y=―x-―+2=―x+―………(答)
4 4 4 4
円x2 +y2 =2の中心(0,0)から切断した直線への
最短距離dは、
|
|<直線とその外の点からの距離の公式>
| 直線の方程式ax+by+c=0、外の点(α,β)のとき、
| |aα+bβ+c|
| d=―――――――――
| √(a2 +b2 )
|
直線の式を変形して、
mx-y-m+2=0より、
|m・0-0-m+2| |2-m|
d=―――――――――――=―――――――
√{m2 +(-1)2 } √(m2 +1)
図の△OAHは直角三角形だから、三平方の定理より、
d2 +12 =(√2)2
∴d2 =1
したがって、
(2-m)2
――――――=1
(m2 +1)
(2-m)2 =(m2 +1)
4-4m+m2 =m2 +1
4m=3
3
∴m=―
4
点P(1,2)を通るから
3
y-2=―(x-1)
4
3 3 3 5
y=―x-―+2=―x+―………(答)
4 4 4 4




