質問＜５４４＞２００１／７／１
from=ささ
「最大・最小（領域）」

y=｛-x+2(x≦1)
    2x-1(x＞1),
y=x+k,x=0およびx=3で囲まれた部分の面積を最小にするkの値を求めよ。

という問題ですが、ハッキリ言ってどこから手をつけていいのかすら分
かりません。

数学の先生が苦手で聞きに行きたくありません（汗）。
教えて頂けると助かります。

お返事２００１／７／５
from=武田

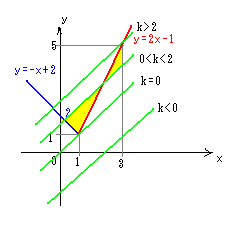①ｋ≦０のとき、
Ｓ＝Ｓ1 ＋Ｓ2 

　　１　　　　　　　　　　　　　　　　　３
　＝∫｛（－ｘ＋２）－（ｘ＋ｋ）｝ｄｘ＋∫｛（２ｘ－１）－（ｘ＋ｋ）｝ｄｘ
　　０　　　　　　　　　　　　　　　　　１

　＝３－３ｋ

②０＜ｋ＜２のとき、
交点を求めると、
｛ｙ＝－ｘ＋２
｛ｙ＝ｘ＋ｋ

　　　２－ｋ
∴ｘ＝────
　　　　２

｛ｙ＝２ｘ－１
｛ｙ＝ｘ＋ｋ

∴ｘ＝１＋ｋ

Ｓ＝Ｓ1 ＋Ｓ2 ＋Ｓ3 ＋Ｓ4 

　　(2-k)/2　　　　　　　　　　　　　　　１
　＝∫｛（－ｘ＋２）－（ｘ＋ｋ）｝ｄｘ＋∫｛（ｘ＋ｋ）－（－ｘ＋２）｝ｄｘ
　　０　　　　　　　　　　　　　　　　　(2-k)/2

　　　1+k　　　　　　　　　　　　　　　　　３
　　＋∫｛（ｘ＋ｋ）－（２ｘ－１）｝ｄｘ＋∫｛（２ｘ－１）－（ｘ＋ｋ）｝ｄｘ
　　　１　　　　　　　　　　　　　　　　　1+k

　　３ｋ2 －６ｋ＋６
　＝────────
　　　　　２

③ｋ≧２のとき、
Ｓ＝Ｓ1 ＋Ｓ2 

　　１　　　　　　　　　　　　　　　　　３
　＝∫｛（ｘ＋ｋ）－（－ｘ＋２）｝ｄｘ＋∫｛（ｘ＋ｋ）－（２ｘ－１）｝ｄｘ
　　０　　　　　　　　　　　　　　　　　１

　＝３ｋ－３


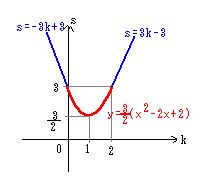　　　　　　　　　　　　　　　　　　３
グラフより、ｋ＝１のとき、最小値Ｓ＝─　……（答）
　　　　　　　　　　　　　　　　　　２