




質問<515>2001/6/14
from=あつ
「ベクトル」
問題;3次元空間において
O(0,0,0)A(0,1,1)B(1、-1、-1)C(5,4,3)がある。
四面体OABCの体積を求めよ。
この前に、OAベクトルとOBベクトルの内積やSin∠AOBの値、
△OABの面積、OAベクトルとOBベクトルに直交する単位ベクトル
を求める問題があります。
それはできましたが、これは・・・。
OABを底面と見たら、高さが分からないので、
それをどうやって出したらいいのでしょうか?
お願いします。
お返事2001/6/15
from=武田
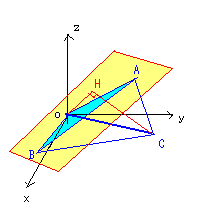 底面OABへ点Cから下ろした足をHとすると、
─→ ─→ ─→
CH=OH-OC
─→ ─→ ─→
OH=sOA+tOB
=s(0 1 1)+t(1 -1 -1)
=(t s-t s-t)
─→
CH=(t s-t s-t)-(5 4 3)
=(t-5 s-t-4 s-t-3)
─→ ─→ ─→ ─→
CH⊥OA、CH⊥OBより、内積を計算すると、
0・(t-5)+1・(s-t-4)+1・(s-t-3)=0
∴2s-2t-7=0……①
1・(t-5)-1・(s-t-4)-1・(s-t-3)=0
∴-2s+3t+2=0……②
①+②より、
t-5=0
∴t=5
したがって、
2s-10-7=0
2s=17
17
∴s=──
2
─→ 17 17
CH=(5-5 ──-5-4 ──-5-3)
2 2
1 1
=(0 -─ ─ )
2 2
したがって、高さ
─→ 1 1
|CH|=√{02 +(-─)2 +(─)2 }
2 2
2 √2
=√(─)=──
4 2
√2
底面積△OAB=──(この前に解いていると思うが……?)
2
したがって、
四面体の体積は、三角錐より、
1 √2 √2 2 1
V=─・──・──=──=─ ……(答)
3 2 2 12 6
底面OABへ点Cから下ろした足をHとすると、
─→ ─→ ─→
CH=OH-OC
─→ ─→ ─→
OH=sOA+tOB
=s(0 1 1)+t(1 -1 -1)
=(t s-t s-t)
─→
CH=(t s-t s-t)-(5 4 3)
=(t-5 s-t-4 s-t-3)
─→ ─→ ─→ ─→
CH⊥OA、CH⊥OBより、内積を計算すると、
0・(t-5)+1・(s-t-4)+1・(s-t-3)=0
∴2s-2t-7=0……①
1・(t-5)-1・(s-t-4)-1・(s-t-3)=0
∴-2s+3t+2=0……②
①+②より、
t-5=0
∴t=5
したがって、
2s-10-7=0
2s=17
17
∴s=──
2
─→ 17 17
CH=(5-5 ──-5-4 ──-5-3)
2 2
1 1
=(0 -─ ─ )
2 2
したがって、高さ
─→ 1 1
|CH|=√{02 +(-─)2 +(─)2 }
2 2
2 √2
=√(─)=──
4 2
√2
底面積△OAB=──(この前に解いていると思うが……?)
2
したがって、
四面体の体積は、三角錐より、
1 √2 √2 2 1
V=─・──・──=──=─ ……(答)
3 2 2 12 6
お便り2001/6/22~24
from=Hideo Nakayama
Regarding to Problem No. 515, I found another solution. I have problems of
writing mathematical expression with symbols; therefore, I substitute with
my own symbols as shown below:
OA a vector of O-to-A
OB a vector of O-to-B
OC a vector of O-to-C
ABS(OA) absolute value or magnitude of a vector 'OA'
I, J, and K unit vectors in x-, y-, and z-axis directions,
respectively
N a unit vector perpendicular to a plane including O,
A, and B
X a cross product of two vectors (Gaiseki in Japanese?)
* a dot product of two vectors (Naiseki in Japanese?)
Consider vector multiplication of (OA X OB) * OC.
where OA = J + K, OB = I - J - K, and OC = 5I + 4J + 3K
Since OA X OB = N (2 times area of triangle OAB)
and N * OC = height of C to the base triangle OAB
The volume of a cone is given by
Vol = (base area) times (height) divided by 3
= ABS(((OA X OB) / 2) * OC) / 3
| I J K |
= ABS (| 0 1 1 | * (5I + 4J + 3K)) / 6
| 1 -1 -1 |
= ABS((J - K) * (5I + 4J + 3K)) / 6
= 1/ 6 ..........Answer





 底面OABへ点Cから下ろした足をHとすると、
─→ ─→ ─→
CH=OH-OC
─→ ─→ ─→
OH=sOA+tOB
=s(0 1 1)+t(1 -1 -1)
=(t s-t s-t)
─→
CH=(t s-t s-t)-(5 4 3)
=(t-5 s-t-4 s-t-3)
─→ ─→ ─→ ─→
CH⊥OA、CH⊥OBより、内積を計算すると、
0・(t-5)+1・(s-t-4)+1・(s-t-3)=0
∴2s-2t-7=0……①
1・(t-5)-1・(s-t-4)-1・(s-t-3)=0
∴-2s+3t+2=0……②
①+②より、
t-5=0
∴t=5
したがって、
2s-10-7=0
2s=17
17
∴s=──
2
─→ 17 17
CH=(5-5 ──-5-4 ──-5-3)
2 2
1 1
=(0 -─ ─ )
2 2
したがって、高さ
─→ 1 1
|CH|=√{02 +(-─)2 +(─)2 }
2 2
2 √2
=√(─)=──
4 2
√2
底面積△OAB=──(この前に解いていると思うが……?)
2
したがって、
四面体の体積は、三角錐より、
1 √2 √2 2 1
V=─・──・──=──=─ ……(答)
3 2 2 12 6
底面OABへ点Cから下ろした足をHとすると、
─→ ─→ ─→
CH=OH-OC
─→ ─→ ─→
OH=sOA+tOB
=s(0 1 1)+t(1 -1 -1)
=(t s-t s-t)
─→
CH=(t s-t s-t)-(5 4 3)
=(t-5 s-t-4 s-t-3)
─→ ─→ ─→ ─→
CH⊥OA、CH⊥OBより、内積を計算すると、
0・(t-5)+1・(s-t-4)+1・(s-t-3)=0
∴2s-2t-7=0……①
1・(t-5)-1・(s-t-4)-1・(s-t-3)=0
∴-2s+3t+2=0……②
①+②より、
t-5=0
∴t=5
したがって、
2s-10-7=0
2s=17
17
∴s=──
2
─→ 17 17
CH=(5-5 ──-5-4 ──-5-3)
2 2
1 1
=(0 -─ ─ )
2 2
したがって、高さ
─→ 1 1
|CH|=√{02 +(-─)2 +(─)2 }
2 2
2 √2
=√(─)=──
4 2
√2
底面積△OAB=──(この前に解いていると思うが……?)
2
したがって、
四面体の体積は、三角錐より、
1 √2 √2 2 1
V=─・──・──=──=─ ……(答)
3 2 2 12 6




