質問＜３２６＞２０００／９／２３
from=瀬能結城
「軌跡」

いつもお世話になっています。
軌跡の問題なのですが、
①直線 y=-2mx+2 と放物線 y=-2x２乗+4x+3 の交点をP,Qとする。
そのとき、任意の実数mに対して、線分P,Qの中点の軌跡を求めなさい

②放物線 C;y=x２乗 と直線l;y=m(x-1) は相異なる２点A,Bで交わっている。
mの値が変化する時、線分ABの中点の軌跡を求めよ。

お返事２０００／９／２４
from=武田

問１

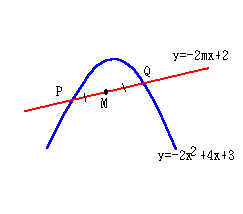交点Ｐ，Ｑは、連立
｛ｙ＝－２ｍｘ＋２
｛ｙ＝－２ｘ2 ＋４ｘ＋３
を解くと求まるので、
－２ｍｘ＋２＝－２ｘ2 ＋４ｘ＋３
２ｘ2 －２（ｍ＋２）ｘ－１＝０
判別式Ｄ／４＝（ｍ＋２）2 ＋２
すべての実数ｍに対して、
Ｄ／４＞０より、異なる実数解が必ず２つある。
その２解をα、βとすると、
中点のｘ座標は
　　α＋β　１　　　－２（ｍ＋２）　　ｍ＋２
ｘ＝───＝─・｛－───────｝＝───
　　　２　　２　　　　　　２　　　　　　２
ｙ＝－２ｍｘ＋２に代入して、

　　　　　　　ｍ＋２
ｙ＝－２ｍ（─────）＋２＝－ｍ（ｍ＋２）＋２＝－ｍ2 －２ｍ＋２
　　　　　　　　２
中点Ｍの座標は
　　　ｍ＋２
Ｍ（─────，－ｍ2 －２ｍ＋２）
　　　　２

このｘ座標とｙ座標より、
２ｘ＝ｍ＋２
ｍ＝２ｘ－２
ｙ＝－ｍ2 －２ｍ＋２
　＝－（２ｘ－２）2 －２（２ｘ－２）＋２
　＝－４ｘ2 ＋８ｘ－４－４ｘ＋４＋２
　＝－４ｘ2 ＋４ｘ＋２
したがって、
中点Ｍが描く軌跡の方程式はｙ＝－４ｘ2 ＋４ｘ＋２……（答）

問２

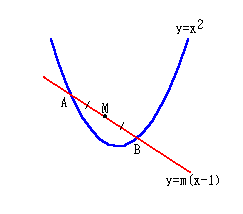交点Ａ，Ｂは、連立
｛ｙ＝ｍ（ｘ－１）
｛ｙ＝ｘ2 
を解くと求まるので、
ｍ（ｘ－１）＝ｘ2 
ｘ2 －ｍｘ＋ｍ＝０
判別式Ｄ＝ｍ2 －４ｍ
２つの異なる実数解をもつには、Ｄ＞０より、
ｍ（ｍ－４）＞０
∴ｍ＜０，４＜ｍ
その２解をα、βとすると、
中点のｘ座標は
　　α＋β　１　　　－ｍ　　ｍ
ｘ＝───＝─・（－──）＝─
　　　２　　２　　　　１　　２
ｙ＝ｍ（ｘ－１）に代入して、

　　　　ｍ　　　　ｍ（ｍ－２）
ｙ＝ｍ（─－１）＝──────
　　　　２　　　　　　２
中点Ｍの座標は
　　　ｍ　　ｍ（ｍ－２）
Ｍ（───，──────）
　　　２　　　　２

このｘ座標とｙ座標より、
２ｘ＝ｍ
ｍ＜０，４＜ｍより、
２ｘ＜０，４＜２ｘ
ｘ＜０，２＜ｘ
代入して
　　２ｘ（２ｘ－２）
ｙ＝────────
　　　　　２

　＝ｘ（２ｘ－２）
　＝２ｘ2 －２ｘ

したがって、
中点Ｍが描く軌跡の方程式は
ｙ＝２ｘ2 －２ｘ
ただし、ｘ＜０，２＜ｘ　　　　……（答）