




質問<3239>2006/6/11
次の問題を教えて下さい。 不良率0.2の製品を100個ずつ箱詰めにする。1箱中の不良品の個数を表す確立をxとする。 1箱中に不良品が高々1個しか含まれない確立を求めよ。 これはポアソン分布を使ったらいいのでしょうか? ★完全解答希望★
お便り2006/6/12
from=亀田馬志
>これはポアソン分布を使ったらいいのでしょうか? いやいや、そんなに難しく考える必要性はありません。 次のように考えて行きます。 >不良率0.2の製品を100個ずつ箱詰めにする。 これだけの情報で、使用する分布を「二項分布」とします。 恐らく、古典的な確率・統計の教科書の流れとしては「正規分布を使え」と言った意図なん でしょうけど、それはあくまで「近似」なんで、これだけパソコンが普及していると、 二項分布の計算は簡易に行えるので、特に近似する必要性は無いと思います。 いずれにせよ、母数(パラメータ)pが0.2と言う母集団から100個無作為抽出する、と言う のがポイントとなります。 つまり、試行回数が100と言った情報と合わせて考えてみると、nからx取る組み合わせ数を combination(n,x)と表記するとして、 p(x)=combination(100,x)*(1/2)^x*(1/2)^(100-x) =combination(100,x)*(1/2)^100 =7.888609×10^(-31)×combination(100,x) を利用する分布とします。 >1箱中の不良品の個数を表す確立をxとする。 >1箱中に不良品が高々1個しか含まれない確立を求めよ。 アトはx=1を上で求めたp(x)に代入して計算すればイイだけ、です(ちょっと珍しい問題 ですがね。通常だったら、不良品が1個以下、と訊くのが多いんですが)。 答えはぶっちゃけると、 5.092590×10^(-07)% となります。 Microsoft Excelで計算する時の書式は、 =binomdist(1,100,0.2,false) となります。試してみてください。
お便り2006/6/14
from=みんみ
亀田馬志さん 回答ありがとうございます。再質問させてください。 パソコンを使わずに出さなくてはいけないのですが、不良率0.2の製品を100個ずつ箱詰め にする。を「二項分布」とするとB(100、1/5)となり、亀田さんが書いてくれていた試行 回数が100と言った情報と合わせて考えてみると、nからx取る組み合わせ数を combination(n,x)と表記するとして、 p(x)=combination(100,x)*(1/2)^x*(1/2)^(100-x) =combination(100,x)*(1/2)^100 =7.888609×10^(-31)×combination(100,x) を利用する分布とします。 の部分ですが、私はp(x)=combination(100,x)*(1/5)^x*(4/5)^(100-x)としたのですが、 1/2になるのか教えてください。また、パソコン使用じゃない場合、この大きな数をどう 計算したらいいのでしょうか。
お便り2006/6/15
from=亀田馬志
おっと、仰るとおりです。
>私はp(x)=combination(100,x)*(1/5)^x*(4/5)^(100-x)とした
その通りですね。
おかしいな。何で1/2なんて書いちゃったのかしら?
解はパソコンで出してるので間違ってないんですが、記述ミスのようです。
多分「チンパンニュースチャンネル」なんか見ながらキー打ってたからだと思います(苦笑)。
かたじけない。
もう一箇所記述ミスがありました。
combination(100,1)=100
なんですね。conbin(n,x)=n!/{(n-x)!*x!}ですから。
従って与式は
p(1)=100*(1/5)*(4/5)^(99)
=20*(4/5)^99
となります。
さて、
>パソコン使用じゃない場合、この大きな数をどう
計算したらいいのでしょうか。
との事なんですが、上見ても分かるように、単純に
>(4/5)^99
の計算が二項分布の場合ネックなんです。
ただし、原理的にアイディアは「二項分布である」と一応覚えておいて下さい。
あんまり「別の分布」は初めっから考えない。
と言うのも、「二項分布である」時点で、近似式の候補は次の二種類しか存在しないから、
です。
①ポアソン分布
②正規分布
んでどっちにせよ、「自分で計算する」って事は殆どあり得ず、多分、大体の問題の場合、
「数表利用」になる事と思います。
ところで、上の二つの分布を利用する場合、「何でもかんでも二項分布を近似できる」と
言うワケでもありません。一応条件・・・・・・と言うか「近似の為の目安」があるんですね。
んで手元の教科書でそれを探そうと思ったのですが・・・・・記述が無いんですよ(笑)。
と言うのも、「数理統計学」系の本や、もしくは「コンピュータ利用」の統計学の書籍では、
そもそも「近似」する必要性が全然無いんですね(笑)。あくまで問題設定に則ってモデルと
なる分布を選ぶ、ってのが「現代的」な統計手法なんです。近似にやかましく言うのは
「古いタイプ」の教科書なんですね(笑)。
そこで、web上で調べてみると・・・・・・
ポアソン分布の場合:二項分布のnが大きく、pが小さい時パラメータλ=n*pとして
ポアソン分布を用いる
正規分布の場合:二項分布の平均npそしてn(1-p)が5よりも大きい場合、
正規分布N(np,np(1-p))で近似できる
と言うのが一応の「目安」ならしいです。あくまで「目安」ですよ、「目安」。大体ポアソン
分布を見ても「nが大きく、pが小さい」なんて書いてますが、じゃあ、どのくらいのnだっ
たら「大きい」と判別するのか、どのくらいのpだったら「小さい」と判別するのか、
丸っきり分かりません(笑)。この辺りの判断基準はハッキリ言うとかなり「主観」ですね。
ですから、みんみさんのように「計算が大変そうだ」と思うのも十二分な
「ポアソン分布利用」の根拠となり得ます。
正規分布の方はかなりメジャーな「近似法」ではありますが、Nがかなり大きい
(N=10,000~100,000)なんかの場合、逆に近似の具合が悪くなるケースもあるよう
なんで、これはこれで「万能」ってワケでもないのです。
と言うわけで、通常、練習問題なんかの場合、あまりにも曖昧になるのを避ける為、
問題文中に「××分布で近似せよ」と指示しているケースが圧倒的に多い筈なんです。
あくまで「数学的」に考える以上、「近似」は「近似以上でも以下でもなく」、それは
「なるべく正確な答えを求めたい」と言った思想には反します。
とまあ、メジャーな近時法を2種類挙げましたが、ではこの問題の場合どっちの近時法を
使えばイイのでしょうか?
答えを言うと「ポアソン分布」でしょうね。正規分布じゃまずい。「何故か?」と言うと
それは技術的な問題に拠ります。
数表利用するのが古いタイプの教科書のスタイルで、「ポアソン分布表」「正規分布表」
2種類ともありますが、ここで落とし穴があります。「正規分布表」で求められる確率は
あくまで「累積確率」なんです。この問題で訊かれている「確率」を求めるには適さない、
と言うのがその「技術的な理由」です。従って消去法によって、「ポアソン分布」しか近似
としては選択肢がありません。
以上を鑑みると、λ=n*p=100×0.2=20としてのポアソン分布を利用するのが、「計算」
としては妥当な方法でしょう。
Poisson(1)=exp(-20)*20^1/1!
=20/exp(20)
と言うのが「計算」による近似式の「解」です。
一応
Poisson(1)=4.122307e-08
辺りでしょうね。
前回提示したB(100,0.2)の解と比較してみて下さい。ちょっと誤差がありますね(笑)。
でもパソコンを使わないとこれが限界だ、と言う事です。
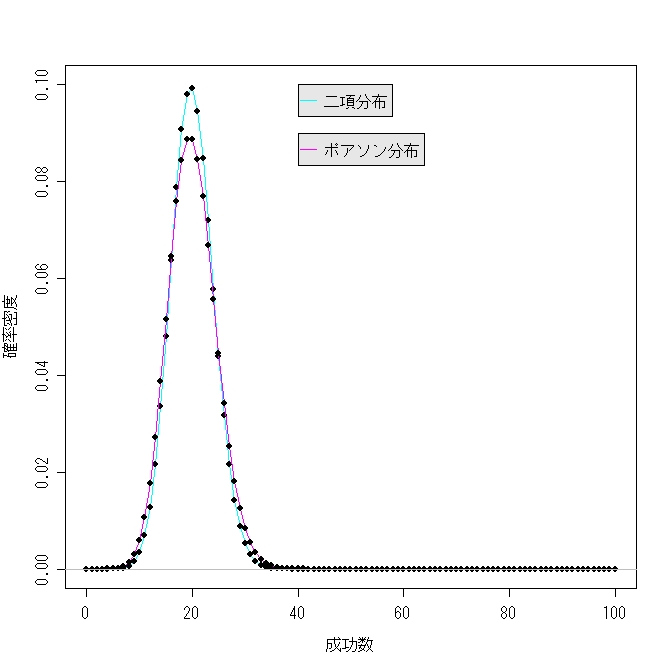
参考までにB(100,0.2)がポアソン分布でどの程度の近似が出来るのか表を掲げておきます。
数値はフリー統計解析ソフトRで計算させたものです。
| x | B(100,0.2) | Poisson(λ=20) |
| 0 | 2.04E-10 | 2.06E-09 |
| 1 | 5.09E-09 | 4.12E-08 |
| 2 | 6.30E-08 | 4.12E-07 |
| 3 | 5.15E-07 | 2.75E-06 |
| 4 | 3.12E-06 | 1.37E-05 |
| 5 | 1.50E-05 | 5.50E-05 |
| 6 | 5.93E-05 | 1.83E-04 |
| 7 | 1.99E-04 | 5.23E-04 |
| 8 | 5.78E-04 | 1.31E-03 |
| 9 | 1.48E-03 | 2.91E-03 |
| 10 | 3.36E-03 | 5.82E-03 |
| 11 | 6.88E-03 | 1.06E-02 |
| 12 | 1.28E-02 | 1.76E-02 |
| 13 | 2.16E-02 | 2.71E-02 |
| 14 | 3.35E-02 | 3.87E-02 |
| 15 | 4.81E-02 | 5.16E-02 |
| 16 | 6.38E-02 | 6.46E-02 |
| 17 | 7.89E-02 | 7.60E-02 |
| 18 | 9.09E-02 | 8.44E-02 |
| 19 | 9.81E-02 | 8.88E-02 |
| 20 | 9.93E-02 | 8.88E-02 |
| 21 | 9.46E-02 | 8.46E-02 |
| 22 | 8.49E-02 | 7.69E-02 |
| 23 | 7.20E-02 | 6.69E-02 |
| 24 | 5.77E-02 | 5.57E-02 |
| 25 | 4.39E-02 | 4.46E-02 |
| 26 | 3.16E-02 | 3.43E-02 |
| 27 | 2.17E-02 | 2.54E-02 |
| 28 | 1.41E-02 | 1.81E-02 |
| 29 | 8.77E-03 | 1.25E-02 |
| 30 | 5.19E-03 | 8.34E-03 |
| 31 | 2.93E-03 | 5.38E-03 |
| 32 | 1.58E-03 | 3.36E-03 |
| 33 | 8.14E-04 | 2.04E-03 |
| 34 | 4.01E-04 | 1.20E-03 |
| 35 | 1.89E-04 | 6.85E-04 |
| 36 | 8.53E-05 | 3.81E-04 |
| 37 | 3.69E-05 | 2.06E-04 |
| 38 | 1.53E-05 | 1.08E-04 |
| 39 | 6.08E-06 | 5.56E-05 |
| 40 | 2.32E-06 | 2.78E-05 |
| 41 | 8.47E-07 | 1.35E-05 |
| 42 | 2.98E-07 | 6.45E-06 |
| 43 | 1.00E-07 | 3.00E-06 |
| 44 | 3.25E-08 | 1.36E-06 |
| 45 | 1.01E-08 | 6.06E-07 |
| 46 | 3.02E-09 | 2.64E-07 |
| 47 | 8.68E-10 | 1.12E-07 |
| 48 | 2.40E-10 | 4.67E-08 |
| 49 | 6.36E-11 | 1.91E-08 |
| 50 | 1.62E-11 | 7.63E-09 |
| 51 | 3.97E-12 | 2.99E-09 |
| 52 | 9.36E-13 | 1.15E-09 |
| 53 | 2.12E-13 | 4.34E-10 |
| 54 | 4.61E-14 | 1.61E-10 |
| 55 | 9.64E-15 | 5.85E-11 |
| 56 | 1.94E-15 | 2.09E-11 |
| 57 | 3.74E-16 | 7.33E-12 |
| 58 | 6.93E-17 | 2.53E-12 |
| 59 | 1.23E-17 | 8.57E-13 |
| 60 | 2.11E-18 | 2.86E-13 |
| 61 | 3.45E-19 | 9.36E-14 |
| 62 | 5.43E-20 | 3.02E-14 |
| 63 | 8.19E-21 | 9.59E-15 |
| 64 | 1.18E-21 | 3.00E-15 |
| 65 | 1.64E-22 | 9.22E-16 |
| 66 | 2.17E-23 | 2.79E-16 |
| 67 | 2.76E-24 | 8.34E-17 |
| 68 | 3.34E-25 | 2.45E-17 |
| 69 | 3.88E-26 | 7.11E-18 |
| 70 | 4.29E-27 | 2.03E-18 |
| 71 | 4.53E-28 | 5.72E-19 |
| 72 | 4.57E-29 | 1.59E-19 |
| 73 | 4.38E-30 | 4.35E-20 |
| 74 | 3.99E-31 | 1.18E-20 |
| 75 | 3.46E-32 | 3.14E-21 |
| 76 | 2.85E-33 | 8.26E-22 |
| 77 | 2.22E-34 | 2.15E-22 |
| 78 | 1.64E-35 | 5.50E-23 |
| 79 | 1.14E-36 | 1.39E-23 |
| 80 | 7.47E-38 | 3.48E-24 |
| 81 | 4.61E-39 | 8.60E-25 |
| 82 | 2.67E-40 | 2.10E-25 |
| 83 | 1.45E-41 | 5.05E-26 |
| 84 | 7.33E-43 | 1.20E-26 |
| 85 | 3.45E-44 | 2.83E-27 |
| 86 | 1.50E-45 | 6.58E-28 |
| 87 | 6.05E-47 | 1.51E-28 |
| 88 | 2.23E-48 | 3.44E-29 |
| 89 | 7.53E-50 | 7.73E-30 |
| 90 | 2.30E-51 | 1.72E-30 |
| 91 | 6.32E-53 | 3.77E-31 |
| 92 | 1.55E-54 | 8.21E-32 |
| 93 | 3.32E-56 | 1.76E-32 |
| 94 | 6.19E-58 | 3.75E-33 |
| 95 | 9.77E-60 | 7.90E-34 |
| 96 | 1.27E-61 | 1.65E-34 |
| 97 | 1.31E-63 | 3.40E-35 |
| 98 | 1.00E-65 | 6.93E-36 |
| 99 | 5.07E-68 | 1.40E-36 |
| 100 | 1.27E-70 | 2.80E-37 |
お便り2006/6/16
from=亀田馬志
あ、アトもう一つ裏ワザがありました。
今後みんみさんが「統計学」を専門に取って行くかどうか分かりませんが(もちろん僕も
統計が専門ではないですが)、数表を使った二項分布を直接計算するテクニックがありま
す。これは確率・統計ではワリとポピュラーな考え方で、場合によってはコンピュータ
ソフトウェアの中でも同様の計算をしてたりします。
これは良く最尤計算に用いられる手法なんですが、確率分布表を用いるのではなく、代わ
りに「常用対数表」を用いる方式です。
例えば、二項分布の場合、
B(n,p)=combination(n,x)*p^x*(1-p)^(n-x)
が方程式ですが、両辺10を底とした対数を取ると、
log|B(n,p)|=log|combination(n,x)*p^x*(1-p)^(n-x)|
となります。
もちろん、確率分布は必ず正の値を取らなければならないので、絶対値記号は意味が無い
のですが、一応定義に従います。
上の式を対数の性質に従ってバラすと、
log|B(n,p)|=log|combination(n,x)|+log|p^x|+log|(1-p)^(n-x)|
=log|combination(n,x)|+x*log|p|+(n-x)*log|1-p|
となるのはお分かりだと思います。
また、
conbin(n,x)=n!/{(n-x)!*x!}
より、
log|conbin(n,x)|=log|n!/{(n-x)!*x!}|
=log|n!|-log|(n-x)!*x!|
=log|n!|-(log|(n-x)!|+log|x!|)
=log|n!|-log|(n-x)!|-log|x!|
となり、
log|n!|=log|n|+log|n-1|+log|n-1|+・・・+log|2|+log|1|
=Σlog|k|・・・(和はk=1からk=n)
log|(n-x)!|=log|n-x|+log|n-x-1|+log|n-x-2|+・・・+log|2|+log|1|
=Σlog|i|・・・(和はi=1からi=n-x)
log|x!|=log|x|+log|x-1|+log|x-2|+・・・+log|2|+log|1|
=Σlog|j|・・・(和はj=1からj=x)
を鑑みると、結果二項分布の対数表示は、
log|B(n,p)|=Σlog|k|-Σlog|i|-Σlog|j|+x*log|p|+(n-x)*log|1-p|
と書き換える事が出来るのです。
この方が常用対数表を使う限り、足し算/引き算だけで済むのでラクと言えばラクなので
す。また、パソコンソフト内でも、combination(n,x)の数値があんまり大きくなるとメモ
リの関係でコンピュータでは扱いづらくなるので、中では対数に変換して足し算で計算し
たアト、底に10を取って指数関数として戻してやる、と言った計算を行っているのです。
(Microsoft Excelでは違うようですがね。だからExcelではあんまり大きな二項分布は計
算できません。)
さて、そうなると、前回の計算のネック、
p(1)=20*(4/5)^99
を常用対数表を用いて計算してみましょう。
log|p(1)|=log|20*(4/5)^99|
=log|20|+log|(4/5)^99|
=log|2^2*5|+99*log|4/5|
=2*log|2|+log|5|+99*(2log|2|-log|5|)
=2*log|2|+log|5|+198*log|2|-99log|5|
=200*log|2|-98log|5|
となります。
常用対数表のlog|2|=0.30103、log|5|=0.69897を利用すると、
log|p(1)|=200×0.30103-98×0.69897
=-8.293061
そして常用対数を元に戻します。
p(1)=10^(-8.293061)
=5.092593×10^(-09)
∴ 5.092593×10^(-07)%
と最初の答えになります。
お便り2006/6/16
from=みんみ
亀田さんいつも丁寧な回答ありがとうございます。 この日曜にテストがありもう一度質問させて下さい。フリー統計解析ソフトRでしようと したのですが、うまく取り込めませんでした。すみません。テストでは数表をみて答える ようになっています。ポアソンの分布表で、m=20、x=1を見たのですが、m=5.0ま でしかない表なのでどう見たらいいのでしょうか。何回も初歩的なことを聞いて申し訳あ りません。
お便り2006/6/18
from=亀田馬志
>この日曜にテストがありもう一度質問させて下さい。
緊急のようなのでコチラの掲示板を使わせていただきます(間に合うかな?)。
>フリー統計解析ソフトRでしようとしたのですが、うまく取り込めませんでした。
タグ内のURLはウィンドウズ専用のRのexe.ファイルです。
ひょっとして使用パソコンがマッキントッシュでしたら、上手く動かないのは当然ですね。
一応Rのインストール方法が紹介されているサイトをご紹介します。
http://www.okada.jp.org/RWiki/index.php?R%20%A4%CE%A5%A4%A5%F3%A5%B9%A5%C8%A1%BC%A5%EB
ここでしたら、Windows版、Mac版、Linux版それぞれのRのインストール方法が紹介されています。
試してみてください。
>テストでは数表をみて答えるようになっています。
でしょうね。ご自分で計算するハメになる事は殆ど無いと思います。
>ポアソンの分布表で、m=20、x=1を見たのですが、m=5.0までしかない表なのでど
う見たらいいのでしょうか。
恐らくそうだと思います。僕の持っている数表でもλ=3.0までしか掲載されていません。
だからこそ、「実計算」に於いては定義通りに計算するしか無いワケですし、そして
ポアソン分布を選んだ理由でもあるのです。
つまり、e=自然対数の底を小数点表示にしない限り、
P(x)=exp(-λ)*λ^x/x!
にx=1、λ=20として
P(1)=20/exp(20)・・・・・・(解)
とここで計算を打ち切っても「数学的には」責められる言われはありません。これは
「数学的」には正しい解だからです。わざわざ小数点表示にする必要性が無い。
ちなみに実は正規分布でも同様の議論が成り立って、「正規分布表」を利用せずとも
(またこの問題の場合は出来ないですが)、定義式通りに
f(x)=1/{√(2π)*4}*exp【-(x-4)^2/{2*4^2}】
としてx=1を代入、つまり
f(1)=1/{√(2π)*4}*exp【-(1-4)^2/{2*4^2}】
=1/{4*√(2π)}*exp【-3^2/{2*16}】
=1/{4*√(2π)*exp(9/32)}・・・(解)
としても「数学的」には責められる言われはないでしょう。
ただし、問題のx=1に於いては、実は正規近似の方がポアソン近似の数値よりは誤差が
大きいです(これはRなんかで計算してみれば一発で分かりますがね)。
お便り2006/6/21
from=みんみ
亀田馬志さん。急な質問にも丁寧に答えていただきありがとうございます。 試験日には見させてもらえなかったのですが、ポアソン分布は出ていませんでした。 しかし、これからのこともあるので、じっくり亀田さんの回答について頭に入れたいと 思います。 本当にありがとうございました。 また、これからもよろしくお願いします。




