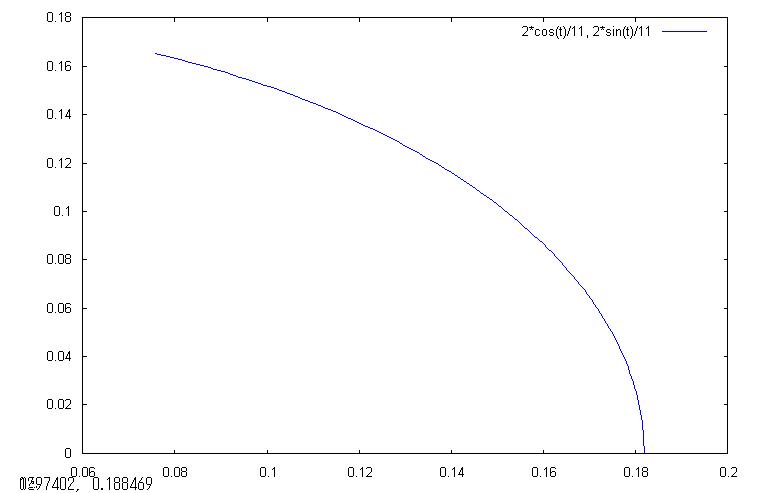
 第2象限
第2象限
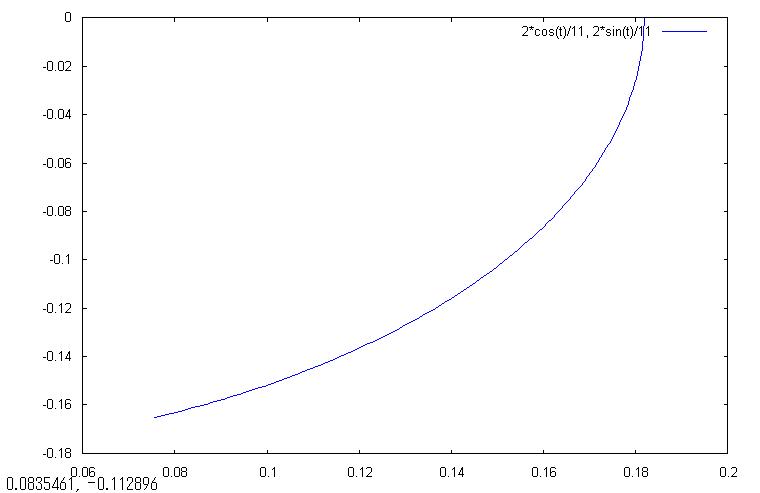 第3象限
第3象限
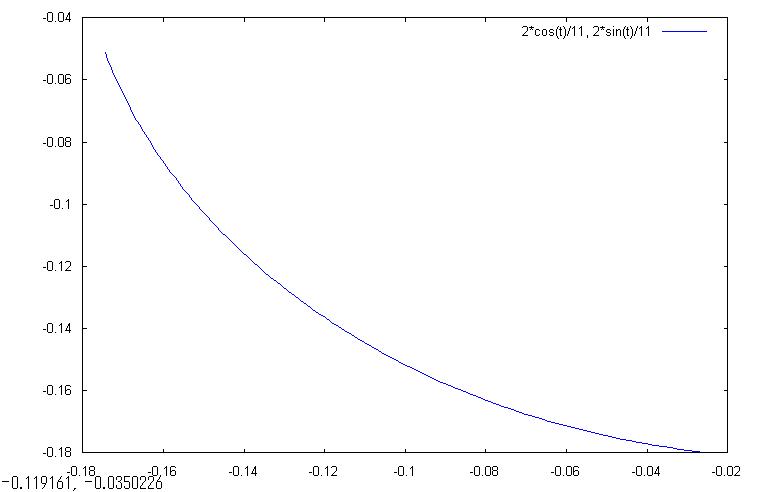 第4象限
第4象限
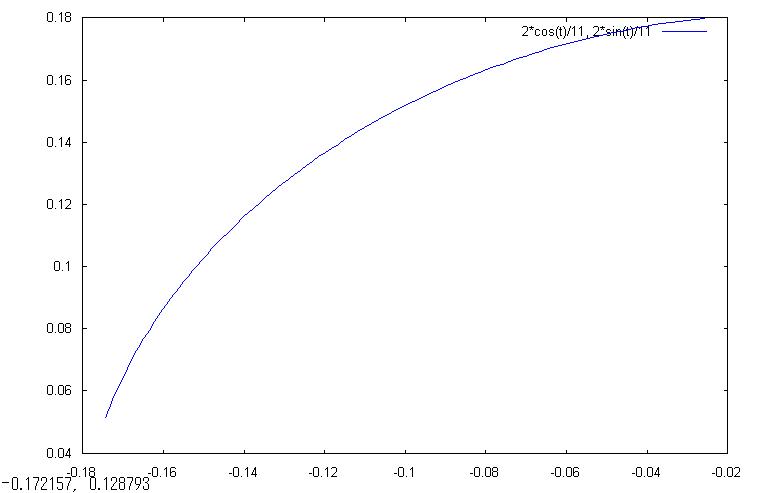 全体図
全体図





質問<3230>2006/6/7
方程式x^11-2=0 1.解をすべて求めよ。 2.Cを複素数平面と見るとき、1.で求めた解のなかで第二象限(実部>0、 虚部<0の領域)に属するものをすべてあげよ。 これってどうやって解くのでしょうか?? よろしくお願いします。 ★完全解答希望★
お便り2006/6/14
from=亀田馬志
分かりません(笑)。全く見当も付きません(笑)。
そこで、手抜きしましょう。フリー数式処理ソフトMAXIMA(Windows版)を使って
解いてみましょうか。数学的な事は分からないんで(笑)、そのテの事は他の得意なお方に
お任せしたいと思います(笑)。
まずは指示に従って、MAXIMA(Windows版)をダウンロードして下さい。
指示通り(と言っても英語ですが、簡単な英語です)MAXIMA(Windows版)をダウン
ロードするとデスクトップ上にMAXIMAのアイコンが出来ている事と思います。
ダブルクリックでMAXIMAを立ち上げてください。
そうすると、次のような画面が現れると思います。
Maxima 5.9.3 http://maxima.sourceforge.net
Using Lisp GNU Common Lisp (GCL) GCL 2.6.7 (aka GCL)
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
This is a development version of Maxima. The function bug_report()
provides bug reporting information.
(%i1)
これでMAXIMAの起動は成功です。そして、(%i1)の後にコマンドを入力して
MAXIMAを動かすワケです。
ではやっていってみましょう。
>方程式x^11-2=0
>1.解をすべて求めよ。
はいはい。
MAXIMAで方程式を解かせるコマンドはsolveコマンドと言って、書式は次の通り
です。
solve(方程式,解きたい文字);
これを最初は(%i1)の後にセミコロン(;)まで入力します。
問題に従うと、次のようになりますね。
(%i1) solve(x^11-2=0,x);
そしてリターンキーを押すと、次のように(%o1)の後にズラズラと数が出てきます。
2 %i %pi 4 %i %pi
-------- --------
1/11 11 1/11 11
(%o1) [x = 2 %e , x = 2 %e ,
6 %i %pi 8 %i %pi
-------- --------
1/11 11 1/11 11
x = 2 %e , x = 2 %e ,
10 %i %pi 10 %i %pi
--------- - ---------
1/11 11 1/11 11
x = 2 %e , x = 2 %e ,
8 %i %pi 6 %i %pi
- -------- - --------
1/11 11 1/11 11
x = 2 %e , x = 2 %e ,
4 %i %pi 2 %i %pi
- -------- - --------
1/11 11 1/11 11 1/11
x = 2 %e , x = 2 %e , x = 2 ]
もの凄い事になってますが(笑)、ちょっと見辛いですが、キチンと解が11個表示されてい
るのが分かると思います。
ネピア数eが底の指数関数をexp()と表記するとして、ちょっと書き直してみましょうか。
x=2^(1/11)*exp(2/11*i*Π)、
2^(1/11)*exp(4/11*i*Π)、
2^(1/11)*exp(6/11*i*Π)、
2^(1/11)*exp(8/11*i*Π)、
2^(1/11)*exp(10/11*i*Π)、
2^(1/11)*exp(-10/11*i*Π)、
2^(1/11)*exp(-8/11*i*Π)、
2^(1/11)*exp(-6/11*i*Π)、
2^(1/11)*exp(-4/11*i*Π)、
2^(1/11)*exp(-2/11*i*Π)、
2^(1/11)
すごいですね。これが解「らしい」です。まあ、バグが無ければこの通りでしょう。
11次方程式なんで、解も全部で11個ですね。
さて、問題2の方にも絡むんですが、この指数関数形式での記述だと大変見辛いです。
なんせ複素数ですからね。そこでオイラーの公式
exp(iθ)=cosθ+isinθ
を利用して、上で出力された解を極形式に変換してみましょう。
MAXIMAでは実部と虚部に複素数を分ける機能があるんで、それを利用してみましょう。
多分(%i2)と言った新しい入力待ちになってるでしょうから、その後に次のよう
セミコロン(;)まで入力します。
(%i2) a:realpart(%o1);
MAXIMAではrealpart(複素数)と言うコマンドが複素数の実部を取り出す命令と
なります。そして、複素数の部分をを前回の計算出力結果%o1で指定しているのです。
また、a:って部分は「aと言う文字に以下の数を代入せよ」と言った意味です。これでaを
使えば計算結果がいつでも復元できるんですね。
リターンキーを押して計算させると、次のような出力が得られます。
1/11 2 %pi 1/11 4 %pi
(%o2) [x = 2 cos(-----), x = 2 cos(-----),
11 11
1/11 6 %pi 1/11 8 %pi
x = 2 cos(-----), x = 2 cos(-----),
11 11
1/11 10 %pi 1/11 10 %pi
x = 2 cos(------), x = 2 cos(------),
11 11
1/11 8 %pi 1/11 6 %pi
x = 2 cos(-----), x = 2 cos(-----),
11 11
1/11 4 %pi 1/11 2 %pi 1/11
x = 2 cos(-----), x = 2 cos(-----), x = 2 ]
11 11
見事に三角関数表記で実部が取り出されました。
では調子にのって虚部も取り出してみましょう。虚部の取り出しコマンドはimagpart
(複素数)です。同様に(%i3)に続いて次のようにセミコロン(;)まで入力します。
(%i3) b:imagpart(%o1);
リターンキーを押すと次の出力が得られます。
(%o3) [0 = 2 sin(-----), 0 = 2 sin(-----),
11 11
1/11 6 %pi 1/11 8 %pi
0 = 2 sin(-----), 0 = 2 sin(-----),
11 11
1/11 10 %pi 1/11 10 %pi
0 = 2 sin(------), 0 = - 2 sin(------),
11 11
1/11 8 %pi 1/11 6 %pi
0 = - 2 sin(-----), 0 = - 2 sin(-----),
11 11
1/11 4 %pi 1/11 2 %pi
0 = - 2 sin(-----), 0 = - 2 sin(-----), 0 = 0]
11 11
またズラズラと出力されました。そしてこれらは既にbに代入されています。
一番最初に複素数で習ったとおり、a+b*iのカタチにしてみます。次のように入力して
下さい。
(%i4) a+b*%i;
MAXIMAでは虚数iや円周率Πのような特殊な数は%piや%iのように表現します
(何故なら、MAXIMAは文字式を扱うので、普通の変数と特殊な定数には違いを持た
せておかないとヤバいからです)。そこで上記のような入力形式を用いるわけです。
リターンキーを押すと次のような計算結果が表示されます。
1/11 2 %pi 1/11 2 %pi
(%o4) [x = 2 %i sin(-----) + 2 cos(-----),
11 11
1/11 4 %pi 1/11 4 %pi
x = 2 %i sin(-----) + 2 cos(-----),
11 11
1/11 6 %pi 1/11 6 %pi
x = 2 %i sin(-----) + 2 cos(-----),
11 11
1/11 8 %pi 1/11 8 %pi
x = 2 %i sin(-----) + 2 cos(-----),
11 11
1/11 10 %pi 1/11 10 %pi
x = 2 %i sin(------) + 2 cos(------),
11 11
1/11 10 %pi 1/11 10 %pi
x = 2 cos(------) - 2 %i sin(------),
11 11
1/11 8 %pi 1/11 8 %pi
x = 2 cos(-----) - 2 %i sin(-----),
11 11
1/11 6 %pi 1/11 6 %pi
x = 2 cos(-----) - 2 %i sin(-----),
11 11
1/11 4 %pi 1/11 4 %pi
x = 2 cos(-----) - 2 %i sin(-----),
11 11
1/11 2 %pi 1/11 2 %pi 1/11
x = 2 cos(-----) - 2 %i sin(-----), x = 2 ]
11 11
これが極形式の表現ですね。
ちょっとWeb上では見辛いかもしれないので、整理しておきましょうか。
x=2^(1/11)*cos(2/11*Π)+2^(1/11)*isin(2/11*Π)、
2^(1/11)*cos(4/11*Π)+2^(1/11)*isin(4/11*Π)、
2^(1/11)*cos(6/11*Π)+2^(1/11)*isin(6/11*Π)、
2^(1/11)*cos(8/11*Π)+2^(1/11)*isin(8/11*Π)、
2^(1/11)*cos(10/11*Π)+2^(1/11)*isin(10/11*Π)、
2^(1/11)*cos(10/11*Π)-2^(1/11)*isin(10/11*Π)、
2^(1/11)*cos(8/11*Π)-2^(1/11)*isin(8/11*Π)、
2^(1/11)*cos(6/11*Π)-2^(1/11)*isin(6/11*Π)、
2^(1/11)*cos(4/11*Π)-2^(1/11)*isin(4/11*Π)、
2^(1/11)*cos(2/11*Π)-2^(1/11)*isin(2/11*Π)、
2^(1/11)
の計11個です。
極形式ですと、角度さえ見ればどの象限に点が存在するのか分かると思うので、
2に対してもこれで探せばイイとは思います。
>2.Cを複素数平面と見るとき、1.で求めた解のなかで第二象限(実部>0、
虚部<0の領域)に属するものをすべてあげよ。
一応プロットするだけしてみましょうか。
実は探したんですが、MAXIMAではComfort Mapping(複素平面描画)の機能がない
みたいなんですね。そこで、代わりにパラメトリック(媒介変数表現)なプロットを試みて
みましょう。
1の解で見る限り、普通の二次元平面で考えると、tをパラメータ(媒介変数)として、
(x,y)=(2^(1/11)*cost,2^(1/11)*sint)
と言った図面を描けば良いわけです。これが複素平面上の
z=2^(1/11)*cosθ+2^(1/11)*isinθ
と図形的には丸っきり同値である、と言うのはお分かりでしょう。
また、cos(-θ)=cos(θ)、sin(-θ)=-sinθより、共役複素数
z'=2^(1/11)*cosθ+2^(1/11)*isinθ
も図形的には特に神経質にならなくっても宜しいと思います。
と言うわけで、MAXIMAで-10/11*π≦t≦10/11*πの範囲の曲線を描いてみましょう。
コマンド形式は
plot2d([parametric,x(t),y(t)],[t,tの最小値,tの最大値],[nticks,100]);
です。最後の[nticks,100]ってのは描画計算エリアの分割数を増やして滑らかなグラフを
描かせるオマジナイみたいなものです。ではやってみましょうか。
(%i5)の後に次のようにセミコロン(;)まで入力します。
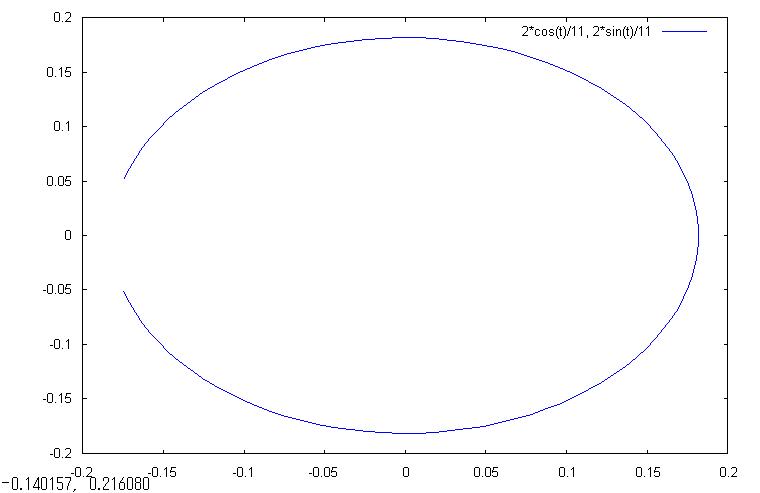
(%i5) plot2d([parametric,2^1/11*cos(t),2^1/11*sin(t)],[t,-10/11*%pi,10/11*%pi],[nticks,100]);
リターンキーを押すとグラフが描画されたと思います。
適当に)[t,tの最小値,tの最大値]の部分を変更して、第二象限(実部>0、虚部<0の
領域)に属するようなグラフを描画する為に色々トライしてみて下さい。
なお、上の完成グラフ(-10/11*π≦t≦10/11*π)は下図の通りです。
第1象限
 第2象限
第2象限
 第3象限
第3象限
 第4象限
第4象限
 全体図
全体図

お便り2006/9/3
from=平 昭
こんにちは。これは、極形式で考えると分かりやすいと思います。 x=r*exp(iθ)=r(cosiθ+isinθ) と置くと(r>0とする) x^11=r^11exp(11iθ) だから、r^11=2、 11θ=2nπ (nは整数) となればよい。 ここで、元の方程式の解は11個であることを考えて x=αexp(2nπi/11) (αは2の11乗根、nは0から10までの整数) となる。 解が第二象限にあるのは、 π/2<2nπ/11<πの時で、つまり、n=3、4、5。 求める解は x=αexp(6πi/11)、αexp(8πi/11)、αexp(10πi/11) となる。




