質問

こんにちわ。ぷりんです。早速ですが質問させて下さい。学校でやった
問題です。
先生に授業で教えてもらったのですがいまいちよくわかりませんでした。

（問）２本の当たりくじをふくむ６本のくじからまずＡが１本ひく。
続いてＢが１本ひき、それがはずれくじならもう１本ひく。
Ａが当たりくじを引いたときはＡが３０００円、
Ｂが当たりくじを引いたときはＢが１５００円の賞金を受け取るとき、
Ａ・Ｂそれぞれが受け取る金額の期待値を求めよ。
ただし、いずれの場合も引いたくじは元に戻さない。 

（授業のノート）
　　６本中２本が当たり。当たり→a・はずれ→bとすると、くじの中身は
　　　（a1・a2・b1・b2・b3・b4）となる。
　　　　①Ａが１本引く　　　　　　　　　　　　　　　
　　　　②Ｂが１本引く。はずれの時もう１本ひく。 
　賞金・Ａ・３０００円
　　　　Ｂ・１５００円
　　　　　　　　　　　　　　　　　　　　　　２　　　１
　　　ⅰ・Ａの当たる事象をＡとするとP(A)＝───＝───
　　　　　　　　　　　　　　　　　　　　　　６　　　３
　　　　　　　　　　　　　　　　　１
　　　　　Ａの期待値は３０００×───＝１０００（円）……Ａの方の答え
　　　　　　　　　　　　　　　　　３ 
　　　ⅱ・Ｂの当たる事象をＢとする。
　　　　図・【考えられる全てのパターン】
　　　（Ａ・Ｂ1・Ｂ2）＝（当たり・当たり・　　　）（当たり・はずれ・当たり）
　　　　　　　　　　　　（当たり・はずれ・はずれ）（はずれ・当たり・　　　）
　　　　　　　　　　　　（はずれ・はずれ・当たり）（はずれ・はずれ・はずれ） 
　　　　　P(B)を出すのだか上記の図から直接Ｂを出すには４つの場合分けが必要
　　　　　となり１からＢバーを引いた方が早い。 
　　　　　Ｂバーのパターン【全事象は２つとも6Ｐ3である】
　　　　　　　　①（当たり・はずれ・はずれ）
　　　　　　　　　　2Ｐ1×4Ｐ2＝２４
　　　　　　　　②（はずれ・はずれ・はずれ）
　　　　　　　　　　4Ｐ3＝２４ 
　　　　　　　　　４８　　　２　　　　　　　　　　　　　　３
　　　　　　　　────＝────……Ｂバー　　∴P(B)＝───
　　　　　　　　１２０　　　５　　　　　　　　　　　　　　５ 
　　　　　　　　　　　　　　　　　３
　　　　　Ｂの期待値は１５００×───＝９００（円）……Ｂの方の答え
　　　　　　　　　　　　　　　　　５ 
          （質問）この【全事象は２つとも6Ｐ3である】の部分で
　　　　　　6Ｐ3だと（当たり・当たり・　　　）と（はずれ・当たり・　　　）
　　　　　　がそれぞれ３回目も引いているカウントになっちゃうからだめなのでは
　　　　　　ないでしょうか？なぜ6Ｐ3になるのかできるだけ詳しく教えて下さい。

お返事２０００／９／２０
from=武田


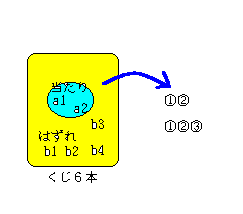６本のくじから１番目にＡが引き、２番目にＢが引き、もしはずれの時は
もう一回３番目のくじを引くと言う問題である。すべての可能性を書きだ
してみると、
　　Ａ　　Ｂ₁　Ｂ₂　
①　○　　○
②　○　　×　　○
③　○　　×　　×
④　×　　○
⑤　×　　×　　○
⑥　×　　×　　×
以上６通りの場合がある。すべての場合を網羅したので、このすべてが起
こる確率は１となる。
この問題は場合によって、確率の計算が少しづつ異なるので、１つ１つ計
算してみよう。
　　　　　　₂Ｐ₂　２・１　　１
①の場合は、───＝───＝──
　　　　　　₆Ｐ₂　６・５　１５

　　　　　　₂Ｐ₁・₄Ｐ₁・₁Ｐ₁　　２・４・１　　１
②の場合は、───────────＝─────＝──
　　　　　　　　　　₆Ｐ₃　　　　　６・５・４　１５

　　　　　　₂Ｐ₁・₄Ｐ₂　　２・４・３　１
③の場合は、───────＝─────＝─
　　　　　　　　₆Ｐ₃　　　６・５・４　５

　　　　　　₄Ｐ₁・₂Ｐ₁　　４・２　４
④の場合は、───────＝───＝──
　　　　　　　　₆Ｐ₂　　　６・５　１５

　　　　　　₄Ｐ₂・₂Ｐ₁　　４・３・２　１
⑤の場合は、───────＝─────＝─
　　　　　　　　₆Ｐ₃　　　６・５・４　５

　　　　　　₄Ｐ₃　４・３・２　１
⑥の場合は、───＝─────＝─
　　　　　　₆Ｐ₃　６・５・４　５

　　　　１　　１　１　　４　１　１　１＋１＋３＋４＋３＋３　１５
なお、──＋──＋─＋──＋─＋─＝───────────＝──＝１
　　　１５　１５　５　１５　５　５　　　　　１５　　　　　　１５

Ａが当たる確率は①②③より、
　　　　　　１　　１　１　１＋１＋３　　５　１
Ｐ（Ａ）＝──＋──＋─＝─────＝──＝─
　　　　　１５　１５　５　　　１５　　１５　３
Ｂが当たる確率は①②④⑤より、
　　　　　　１　　１　　４　１　１＋１＋４＋３　　９　３
Ｐ（Ｂ）＝──＋──＋──＋─＝───────＝──＝─
　　　　　１５　１５　１５　５　　　１５　　　　１５　５

Ａの期待値は、３，０００円×１／３＝１，０００円
Ｂの期待値は、１，５００円×３／５＝　　９００円

さて、質問の【全事象は２つとも６Ｐ３である】だが、
　　　　　　　　　＿
Ｐ（Ｂ）＝１－Ｐ（Ｂ）　　　　　　＿
つまり、上の③と⑥の計算から、Ｐ（Ｂ）を出すのだが、
この③と⑥の分母が、このときの全事象の個数だから₆Ｐ₃となっている。
これは、①「当たり・当たり・　　　」と④「はずれ・当たり・　　　」
のときの全事象の個数とは違う。ちなみにこちらは₆Ｐ₂である。