質問

次の関数が単調減少であることを証明せよ。

f(x)=x^(1/x)  (x＞0)

を教えてください。宜しくお願いします。

★希望★完全解答★

お便り２００５／１０／１２
from=wakky

問題はこれでいいですか？
ｆ（ｘ）＝ｘの（1/ｘ）乗ってことでしょうか？
両辺の自然対数をとって、微分するとわかりますが、
単調減少にならないのでは？
たとえば
ｘ＝1のときｆ（1）＝1＾1＝1
ｘ＝2のときｆ（2）＝2＾（1/2）＝√2
つまりｆ（1）＜ｆ（2）ですから
どこかで増加していることになります。
ｘ＞0では連続なので、単調減少ではなさそうです。

お便り２００５／１０／１３
from=UnderBird

f(x)=x^(1/x)  (x＞0)
ではなく、
f(x)=x^(1/x)  (x＞e)
ではないですか。
両辺の対数をとって、微分→増減表
でよいのではないでしょうか？

お返事２００５／１０／１３
from=武田

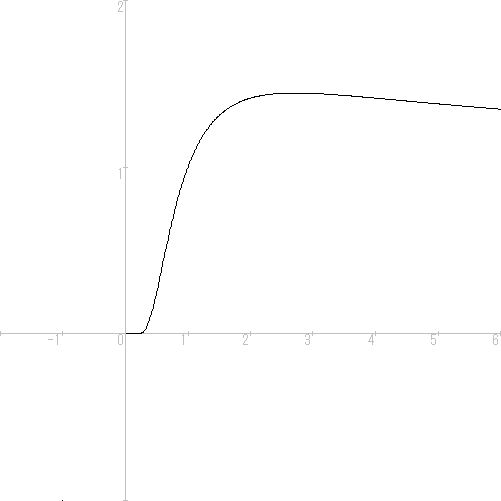
作図したら
ｘ＞ｅ（約２．７１８）で単調減少になっていました。