




質問<226>2000/2/6
from=mebius
「平面と直線の交点」
先ず
平面の方程式の一般形
Ax+By+Cz+D=0
直線の方程式
(x,y,z)=(a,b,c)+t(d,e,f)
とした上で、代入法により
tについて
-(Aa+Bb+Cc+D)
t = --------------
(Ad+Be++Cf)
このtを直線の方程式に代入すると交点が
求まるものと思います。
疑問はここからでして
平面の方程式の(A,B,C)は法線ベクトル
Dは法線ベクトル方向の原点からの距離と認識していました。
例えば
三角形
A(-10, 10, 0)
B( 0, 10,10)
C( 10, 10, 0)
の法線ベクトルが(0,1,0)とすると
Dは平面上に含まれる一点を用いて求めることができるので
10になります。
直線の開始点を(0,15,0)、方向を(0,-1,0)とすると
前述の認識では交点の結果がおかしくなります。
そこで平面式の一般形を
D = -(Ax+By+Cz)
と変形してから当てはめてやると全く問題はなくなるの
ですが、今度は
Dは法線ベクトル方向の原点からの距離と認識
していたものと違うことになります。
一体Dとはどういう意味なのでしょうか?
また、とある参考書を見ると
平面式の一般形が
Ax+By+Cz=D
などと掲載されていたのですが、他のどの参考書を
見てもそんな書き方はされていません。
一体何が真実なのかわからずに困惑しています。
ご教授お願いします。
お返事2000/2/7
from=武田
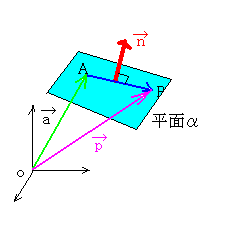 平面αの方程式をAx+By+Cz+D=0とすると、
→
法線ベクトルn=(A,B,C)
平面上の2点A(a,b,c)P(x、y、z)とすると、
原点からの位置ベクトルは、
→ →
p=(x、y、z)、a=(a,b,c)
平面α上の直線は次のベクトルで表示できる。
→ →
p-a=(x-a,y-b,z-c)
このベクトルと、法線ベクトルは垂直だから、
内積がゼロとなる。
→ → →
n・(p-a)=0
A(x-a)+B(y-b)+C(z-c)=0
Ax+By+Cz+(-Aa-Bb-Cc)=0
したがって、一般には、D=(-Aa-Bb-Cc)は原点
と平面との距離と言うことはできない。
D=-(Aa+Bb+Cc)
→ →
=-n・a
→ → → →
aを法線ベクトルnと同方向とすると、a=knより、
→ →
D=-n・kn
→
=-k|n|2
→ →
|n|=1のとき、(nを単位ベクトルとすると)
D=-k
→ →
|a|=k|n|=k
→
D=-|a|
→
Ax+By+Cz-|a|=0
したがって、平面の方程式をAx+By+Cz=Dとし、
法線ベクトルが単位ベクトルとすると、Dは原点からの法線ベクトル方向の平面までの距離と言うことができそうである。
平面αの方程式をAx+By+Cz+D=0とすると、
→
法線ベクトルn=(A,B,C)
平面上の2点A(a,b,c)P(x、y、z)とすると、
原点からの位置ベクトルは、
→ →
p=(x、y、z)、a=(a,b,c)
平面α上の直線は次のベクトルで表示できる。
→ →
p-a=(x-a,y-b,z-c)
このベクトルと、法線ベクトルは垂直だから、
内積がゼロとなる。
→ → →
n・(p-a)=0
A(x-a)+B(y-b)+C(z-c)=0
Ax+By+Cz+(-Aa-Bb-Cc)=0
したがって、一般には、D=(-Aa-Bb-Cc)は原点
と平面との距離と言うことはできない。
D=-(Aa+Bb+Cc)
→ →
=-n・a
→ → → →
aを法線ベクトルnと同方向とすると、a=knより、
→ →
D=-n・kn
→
=-k|n|2
→ →
|n|=1のとき、(nを単位ベクトルとすると)
D=-k
→ →
|a|=k|n|=k
→
D=-|a|
→
Ax+By+Cz-|a|=0
したがって、平面の方程式をAx+By+Cz=Dとし、
法線ベクトルが単位ベクトルとすると、Dは原点からの法線ベクトル方向の平面までの距離と言うことができそうである。





 平面αの方程式をAx+By+Cz+D=0とすると、
→
法線ベクトルn=(A,B,C)
平面上の2点A(a,b,c)P(x、y、z)とすると、
原点からの位置ベクトルは、
→ →
p=(x、y、z)、a=(a,b,c)
平面α上の直線は次のベクトルで表示できる。
→ →
p-a=(x-a,y-b,z-c)
このベクトルと、法線ベクトルは垂直だから、
内積がゼロとなる。
→ → →
n・(p-a)=0
A(x-a)+B(y-b)+C(z-c)=0
Ax+By+Cz+(-Aa-Bb-Cc)=0
したがって、一般には、D=(-Aa-Bb-Cc)は原点
と平面との距離と言うことはできない。
D=-(Aa+Bb+Cc)
→ →
=-n・a
→ → → →
aを法線ベクトルnと同方向とすると、a=knより、
→ →
D=-n・kn
→
=-k|n|2
→ →
|n|=1のとき、(nを単位ベクトルとすると)
D=-k
→ →
|a|=k|n|=k
→
D=-|a|
→
Ax+By+Cz-|a|=0
したがって、平面の方程式をAx+By+Cz=Dとし、
法線ベクトルが単位ベクトルとすると、Dは原点からの法線ベクトル方向の平面までの距離と言うことができそうである。
平面αの方程式をAx+By+Cz+D=0とすると、
→
法線ベクトルn=(A,B,C)
平面上の2点A(a,b,c)P(x、y、z)とすると、
原点からの位置ベクトルは、
→ →
p=(x、y、z)、a=(a,b,c)
平面α上の直線は次のベクトルで表示できる。
→ →
p-a=(x-a,y-b,z-c)
このベクトルと、法線ベクトルは垂直だから、
内積がゼロとなる。
→ → →
n・(p-a)=0
A(x-a)+B(y-b)+C(z-c)=0
Ax+By+Cz+(-Aa-Bb-Cc)=0
したがって、一般には、D=(-Aa-Bb-Cc)は原点
と平面との距離と言うことはできない。
D=-(Aa+Bb+Cc)
→ →
=-n・a
→ → → →
aを法線ベクトルnと同方向とすると、a=knより、
→ →
D=-n・kn
→
=-k|n|2
→ →
|n|=1のとき、(nを単位ベクトルとすると)
D=-k
→ →
|a|=k|n|=k
→
D=-|a|
→
Ax+By+Cz-|a|=0
したがって、平面の方程式をAx+By+Cz=Dとし、
法線ベクトルが単位ベクトルとすると、Dは原点からの法線ベクトル方向の平面までの距離と言うことができそうである。




