質問＜１５３＞９９／６／２２
１）√９７６０００
3
２） √１０００００
３）√０．８８４４
これらを小数点以下４桁まで求めたいのですがどのようにす
ればよいのでしょうか？
何か公式のようなものはないのでしょうか？
今までは、数を少しづつ増やしたり減らしたりしてきたので
すが細かい数字まで求めなければいけない場合は不可能にな
ってきました。
どうか良きアドバイスをお願いします。
お返事９９／６／２３
from=武田
方法としては、４つあると思います。
１つ目は、関数電卓を利用する方法です。私の勤める工業高
校では、数学の時間はいつでも使って良いことにしています。
もし、差し障りがなければこれが一番でしょう。
２つ目は、開平算という２乗根を求める方法です。大変です
が、小数何位まででも求められます。詳しくは、ここの質問
４７に計算方法が書いてありますので参照して下さい。ただ
し、３乗根には使えません。つまり、（１）（３）は解ける
けど、（２）は解けません。
３つ目は、常用対数表を利用するやり方です。（２）を解い
てみましょう。
3
Ｘ＝ √（１０００００） とおく。
ｌｏｇＸ＝（１／３）・ｌｏｇ１０００００
＝（１／３）・５
＝５／３
＝１．６６６６・・・
常用対数表より、
Ｘ＝４６．４１・・・
あれ、このやり方では小数４位まで求めるのは難しそうです
ね。
４つ目は、簡単になるまで変形してから計算する方法です。
（１）を解いてみましょう。
√（９７６０００）＝√（２7・５3・６１）
＝２3・５・√（２・５・６１）
＝４０√６１０
この方法も、最後は関数電卓か、開平算に頼らなくてはなり
ません。
以上４つについて考察してきましたが、小数４位まで求める
のは関数電卓以外は難しそうですね。
こんな結論ではいけませんか？
お返事（追加）９９／６／２７
from=武田
関数電卓や開平算に頼らなくて、さらに３乗根も解ける方法 はないかと調べていたら、ニュートン法というのがありまし た。 関数ｙ＝ｆ（ｘ）の点（ｘ1，ｆ（ｘ1））における 接線の方程式は、 ｙ－ｆ（ｘ1）＝ｆ′（ｘ1）（ｘ－ｘ1） だから この接線とｘ軸が交わる点のｘ座標をｘ2とすると、 ｙ＝０より ０－ｆ（ｘ1）＝ｆ′（ｘ1）（ｘ2－ｘ1） ｘ2－ｘ1＝－ｆ（ｘ1）／ｆ′（ｘ1） ｘ2＝ｘ1－ｆ（ｘ1）／ｆ′（ｘ1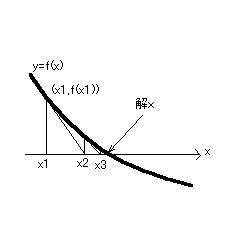）これを繰り返していくと、数列の漸化式ができる。 ｘn+1＝ｘn－ｆ（ｘn）／ｆ′（ｘn） したがって、ｘn+1はだんだんｆ（ｘ）＝０の解ｘに 近づいていく。 これを利用して、平方根や３乗根を求めることができる。 平方根√ａは、 ｆ（ｘ）＝ｘ2－ａより ｆ′（ｘ）＝２ｘ ｘn+1＝ｘn－（ｘn2－ａ）／（２ｘn） ＝（ｘn＋ａ／ｘn）／２ これを利用して質問を解いてみると、 １）√９７６０００ ａ＝９７６０００、ｘ1＝１０００とする。 １０００は２乗するとａに近いから ｘ2＝（１０００＋９７６０００／１０００）／２ ＝９８８ ｘ3＝（９８８＋９７６０００／９８８）／２ ≒９８７．９２７１２５ ｘ4＝（９８７．９２７１２＋９７６０００／９８７．９２７１２）／２ ≒９８７．９２７１２２ ∴√９７６０００＝９８７．９２７１（小数第４位） ３）√０．８８４４ ａ＝０．８８４４、ｘ1＝１とする。 １は２乗するとａに近いから ｘ2＝（１＋０．８８４４／１）／２ ＝０．９４２２ ｘ3＝（０．９４２２＋０．８８４４／０．９４２２）／２ ≒０．９４０４２７ ｘ4＝（０．９４０４２７＋０．８８４４／０．９４０４２７）／２ ≒０．９４０４２５ ∴√０．８８４４＝０．９４０４（小数第４位） ３乗根3√ａは、 ｆ（ｘ）＝ｘ3－ａより ｆ′（ｘ）＝３ｘ2 ｘn+1＝ｘn－（ｘn3－ａ）／（３ｘn2） ＝（２ｘn＋ａ／ｘn2）／３ より 3 ２） √１０００００ ａ＝１０００００、ｘ1＝５０とする。 ５０は３乗するとａに近いから ｘ2＝（２×５０＋１０００００／５０2）／３ ≒４６．６６６６６６ ｘ3＝（２×４６．６６６６６６＋１０００００／４６．６６６６６６2）／３ ≒４６．４１７２３３ ｘ4＝（２×４６．４１７２３３＋１０００００／４６．４１７２３３2）／３ ≒４６．４１５８８８ ｘ5＝（２×４６．４１５８８８＋１０００００／４６．４１５８８８2）／３ ≒４６．４１５８８８ ∴3√１０００００＝４６．４１５９（小数第４位）