質問

だれか判る方、よろしくお願いします。

1. a＞1のとき、次の極限値を求めよ。
　　　　lim[n→∞]［0.n] {1＋(ｘ/ｎ)}^ne^(-ax)dx

2.次の無限級数の和を求めよ。
　ただし、｜x｜＜1、αは実数とする。
　xsin^2（α）-(x^2/2)sin^2（2α）+(x^3/3)sin^2（3α）-・・・

お便り２００３／３／１１
from=juin

1.
a>1のとき、lim[n->∞]∫[0,n]{1+(x/n)}^n*e^(-ax)dx
=∫[0,∞){e^x*e^(-ax)}dx=1/(a-1)

Proof lim[n->∞]{1+(x/n)}^n=e^x  (広義一様収束）
f(x)=e^x*e^(-ax),fn(x)=(1+(x/n))^n*e^(-ax)とする。
|∫[0,∞)fdx-∫[0,n]fndx|　　(*)
＜∫[0,L]|f-fn|dx+∫[L,n]|f-fn|dx+∫[n,∞)fdx
ここで、ε>0に対して、L>0を次のように決める。
∫[L,n]|f-fn|dx+∫[n,∞)fdx＜∫[L,∞)fdx=e^((1-a)L)/(a-1)＜ε
更に、Nを十分大きくとって、
n>Nに対して|f(x)-fn(x)|＜ε/L　x∈[0,L]とする。
(*)＜ε+ε=2ε
よって、lim[n->∞]∫[0,n]{1+(x/n)}^n*e^(-ax)dx
=∫[0,∞){e^x*e^(-ax)}dx=1/(a-1)

お便り２００３／６／２６
from=Tetsuya Kobayashi

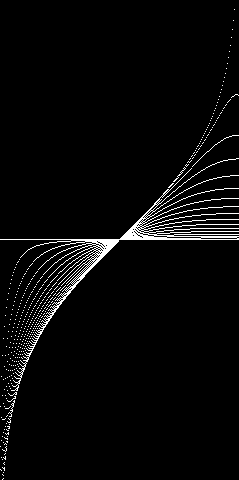
(2)について。
三角関数がかかっていなければただの対数関数なんですが。
いまいちイメージが掴めなかったのでシミュレーションを。
$x$軸にへばりついてるのが$\alpha=0$で、両端が収束して
ないのが$\alpha=\pi/2$です。
やっぱり対数関数に近い感じなんですよねぇ。
でも初等関数でどう表現していいのやら。

お便り２００３／７／７
from=Tetsuya Kobayashi

(2)について。
高木貞治の『解析概論』をめくっていたら
答えが分かったので報告します。

1             (1+x)^2
- log ------------------------
4      1+2x\cos(2\alpha)+x^2

です。