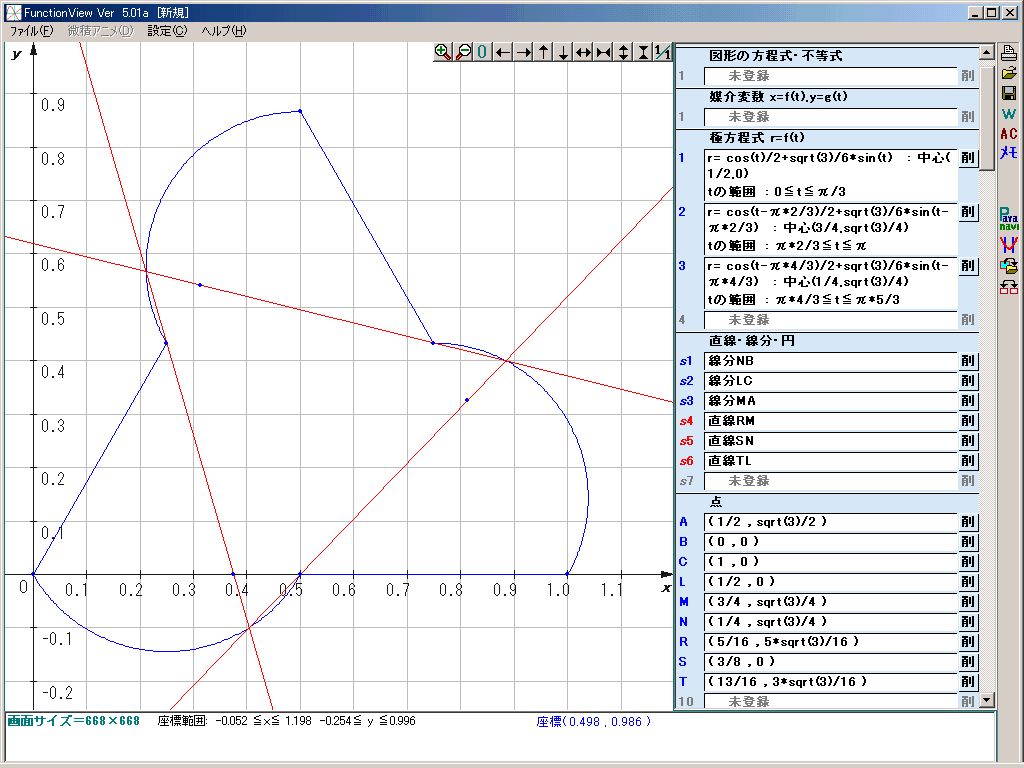
 図の青線で囲まれた部分が求める領域です。
(赤線は三角形DEFの例です。)
曲線部分は極方程式の形式で記述することができます。
面積を計算すると、π/12+(3√3)/16 となるでしょう。
(計算ミスをしている可能性もありますので、あまり信用しないよう。)
図の青線で囲まれた部分が求める領域です。
(赤線は三角形DEFの例です。)
曲線部分は極方程式の形式で記述することができます。
面積を計算すると、π/12+(3√3)/16 となるでしょう。
(計算ミスをしている可能性もありますので、あまり信用しないよう。)





質問<923>2002/8/16
一辺の長さが1の正三角形ABCがある。辺BC,辺CA、辺ABの 中点をそれぞれL、M,Nとし AP=BQ=CR=t となる辺AB上の点をP,辺BC上の点をQ,辺CA上の点をRとし、 直線PM、直線QN,直線RLをそれぞれm1、m2、m3とする。 m1とm2、m2とm3、m3とm1との交点をそれぞれD,E,F とし、三角形DEFを考える。 このときtが0から1まで変化するとき、三角形DEFが通過する領域 を図示しその面積を求めよ。 この問題がわかりません。 お手数ですがなるべくお早めに回答よろしくお願いします
お便り2002/8/18
from=Tetsuya Kobayashi
図の青線で囲まれた部分が求める領域です。 (赤線は三角形DEFの例です。) 曲線部分は極方程式の形式で記述することができます。 面積を計算すると、π/12+(3√3)/16 となるでしょう。 (計算ミスをしている可能性もありますので、あまり信用しないよう。)
お便り2002/8/19
from=mochi
早々にお答えいただいてありがとうございます。 申し訳ありませんが、青い部分の極方程式は どのようにして求められるのでしょうか?
お便り2002/8/19
from=Tetsuya Kobayashi
こんにちは。 LF=r、∠FLC=θとおいたときのrとθの関係を求めてみよう。 ただし、0°≦θ≦60°とする。 対称性より、三角形DEFは正三角形となり、正三角形ABCの重心をG とすると、正三角形DEFの重心もGとなる。 GからLFに下ろした垂線の足をHとする。 Lを原点、LC方向をx軸、LA方向(LG方向)をy軸とするxy直交座標を 考えると、 直線LFの式はy=(tanθ)x、G(0, (√3)/6)となるから、 GとLFの距離すなわちGHの長さは、 点と直線の距離の公式を用い、 また1+(tanθ)^2=1/(cosθ)^2に注意し、 cosθ≧0であることから、 GH=((√3)/6)cosθとなる。 ∠FGH=60°、∠LGH=θであることから、 FH=(1/2)cosθ、LH=((√3)/6)sinθとなり、 LF=(1/2)cosθ+((√3)/6)sinθとなる。 したがって、Lを原点、LC方向を始線とする極座標を考えると、 0°≦θ≦60°のとき、 r=(1/2)cosθ+((√3)/6)sinθ という極方程式でFの軌跡が求まります。 ※ 60°<θ≦90°のとき、正三角形DEFは正三角形ABCに 完全に含まれてしまうので計算しなくていいでしょう。 ※ ちなみに、θ=90°(t=1に相当)のときには 正三角形DEFは存在しませんね。




