質問＜７８＞９８／１１／３
from=みほ
「微分：極値を持つための条件」

こんにちは。
「関数 ｆ(x) = x^3+ax^2+bx+1 (a,bは実数の定数）とすると
き、f(x)がｘ＝１で極値を持つ定数a,bの条件を求めよ。」と
いう問題の解説で、

ｆ｀（１）の符号がｘ＝１の前後で変化するために、
ｆ｀（ｘ）＝０がｘ＝１以外の解を持てばよい
となっているのですが、どういうことなのでしょうか。
教えて下さい。よろしくお願いします。

お返事９８／１１／４
from=武田

f(x)＝ｘ3＋ａｘ2＋ｂｘ＋１がｘ＝１で極値を持つことから、
f'(x)＝３ｘ2＋２ａｘ＋ｂ
f'(1)＝３＋２ａ＋ｂ＝０
∴ｂ＝－２ａ－３……①

また、ｘ＝１で極値を持つことから、例えば、

　ｘ　
………
　１　
………
f'(x)　
　－　
　０　
　＋　

と言う具合に、f'(x)の符号はｘ＝１の左と右では逆の符号と
なる。
f'(x)＝３ｘ2＋２ａｘ＋ｂは二次関数になるので、
グラフを書くと、ｘ＝１の前後でグラフはｘ軸の下と上になる。

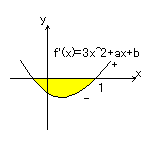したがって、グラフはｘ軸と交わるので、
方程式３ｘ2＋２ａｘ＋ｂ＝０は２つの異なる
実数解をもつ。判別式Ｄ／４＝ａ2－３ｂ＞０
∴ａ2－３ｂ＞０……②

①と②より、
ａ2－３（－２ａ－３）＞０
ａ2＋６ａ＋９＞０
（ａ＋３）2＞０
∴ａ≠－３のすべての実数

したがって、実数ａの条件はａ≠－３
　　　　　　実数ｂの条件はｂ＝－２ａ－３