質問＜５６４＞２００１／７／１１
from=yoshi
「立体の体積」

媒介変数表示ｘ＝sint , y=sin2t , 0≦t≦πで定められる曲線が囲む
部分をCとする。
(1)Cをｘ軸のまわり回転して得られる立体の体積Vxを求めよ。
(2)Cをｙ軸のまわり回転して得られる立体の体積Vyを求めよ。

お返事２００１／７／１２～１４
from=武田

０≦ｔ≦πの範囲で、
媒介変数表示
｛ｘ＝sinｔ
｛ｙ＝sin２ｔ
により書かれたグラフは下図のようになる。



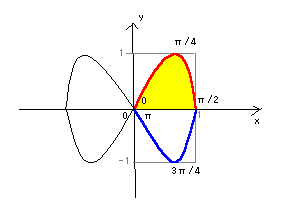ｘ軸のまわりに回転させたときの体積Ｖxは、

　　　　１
Ｖx＝π∫　ｙ2 ｄｘ
　　　　０

　　　　π/2　　　ｄｘ
　　＝π∫　　ｙ2 ───ｄｔ
　　　　０　　　　ｄｔ

　　　　π/2
　　＝π∫　sin2 ２ｔ・cosｔｄｔ
　　　　０

　　　　　π/2
　　＝４π∫　sin2 ｔ・cos2 ｔ・cosｔｄｔ
　　　　　０

　　　　　π/2
　　＝４π∫　（sin2 ｔ－sin4 ｔ）cosｔｄｔ
　　　　　０

　　　　　１
　　＝４π∫　（ｚ2 －ｚ4 ）ｄｚ
　　　　　０

　　　　　　ｚ3 　　ｚ5 　１
　　＝４π［──－──　］
　　　　　　３　　　５　０

　　　　　　１　１　　　８
　　＝４π（─－─）＝──π　……（答）
　　　　　　３　５　　１５

ｙ軸のまわりに回転させたときの体積Ｖyは、

　　　　１
Ｖy＝２∫　２πｘ・ｙｄｘ
　　　　０

　　　　　π/2　　　ｄｘ
　　＝４π∫　ｘ・ｙ──ｄｔ
　　　　　０　　　　ｄｔ

　　　　　π/2
　　＝４π∫　sinｔ・sin２ｔ・cosｔｄｔ
　　　　　０

　　　　　π/2
　　＝４π∫　sinｔ・２sinｔcosｔ・cosｔｄｔ
　　　　　０

　　　　　π/2
　　＝８π∫　sin2 ｔ・cos2 ｔｄｔ
　　　　　０

　　　　　　　sin3 ｔcosｔ　π/2　２－１　π/2
　　＝８π｛［──────］　　＋───　∫　sin2 ｔｄｔ｝
　　　　　　　　２＋２　　　０　　２＋２　０

　　　　　　　　　　１　π/2
　　＝８π（０－０＋─∫　sin2 ｔｄｔ）
　　　　　　　　　　４　０

　　　　　π/2
　　＝２π∫　sin2 ｔｄｔ
　　　　　０

　　　　　　　　sinｔcosｔ　π/2　１　π/2
　　＝２π｛［－─────　］　＋─∫　ｄｔ｝
　　　　　　　　　　２　　　０　　２　０

　　　　　　　　　　１　　π/2　　２π2 　　　π2 
　　＝２π（０－０＋─［ｔ］　）＝───　＝──　……（答）
　　　　　　　　　　２　　０　　　４　　　　　２

※私が出来たのと同時に、ｄ３さんからアドバイスを頂きました。
公式∫sinm ｘcosn ｘｄｘや∫sinm ｘｄｘを使わない点が素晴らしいです。
答えのπ2 ／２が同じなので、安心しました。
ｄ３さん感謝！！

お便り２００１／７／１４
from=ｄ３

質問＜５６４＞の解答です！
ｘ軸に関して対称なグラフですので，
0≦t≦π/2　の部分を2倍すればいいでしょう．
ｙ軸のまわりに回転させたときの体積Ｖyは，
円柱の側面積を集めることを考えれば，

　　 π/2   　dx
Ｖy＝∫2πxy ──dt×2
　 　 0　　  dt

被積分関数は
2πsint・sin2t・cost＝π(sin2t)^2
　　　　　　　　　  ＝π(1－cos4t)/2
　　 π/2　　
Ｖy＝∫π(1－cos4t)dt
　    0　　　　
　　　　
　　＝(π^2)/2