質問＜５５１＞２００１／７／４
from=資格試験受験生
「全微分のイメージ」

武田先生、ご多忙なところ失礼致します。
全微分ｄｚ＝{∂ｚ（ｘ、ｙ）／∂ｘ}・ｄｘ＋{∂ｚ（ｘ、ｙ）／∂ｙ}・ｄｙを、
第一象限において、3次元図でイメージするときについての質問です。

たとえばｚ＝２ｘ＋ｙという関数なら、
∂ｚ（ｘ、ｙ）／∂ｘ＝２、∂ｚ（ｘ、ｙ）／∂ｙ＝１というのが、
３次元の図でイメージできるのですが、
たとえばｚ＝２ｘｙというものですと、
∂ｚ（ｘ、ｙ）／∂ｘ＝２ｙ、∂ｚ（ｘ、ｙ）／∂ｙ＝２ｘというのが、
ちょっとよくイメージできません。
単に、∂ｚ（ｘ、ｙ）／∂ｘ＝２ｙならば、たとえばｙ＝２のとき、
ｘが1単位増加すると、ｙである２も掛けられるという形で、
点をプロットして３次元図を描けばよいのでしょうか？

また、ｚ＝２ｘ＋ｙのときは、ｘ軸上でも、y軸でもｚの値がプラスで、
ｚ＝２ｘｙのときはｘ軸上でもｙ軸上でもゼロでイメージすればよいのでしょうか？

お返事２００１／７／５
from=武田

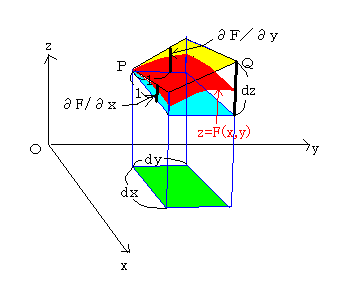
全微分を３次元的にイメージすると、下図のようになる。


ｚ＝２ｘ＋ｙは平面だから、その平面上の１点（ｘ，ｙ，ｚ）をとったとき、
その点における接平面はもとの平面と一致する。
その接平面におけるｚ増分は、ｄｚ＝２・ｄｘ＋１・ｄｙとなる。

ｚ＝２ｘｙは曲面だから、その曲面上の１点（ｘ，ｙ，ｚ）をとったとき、
その点における接平面をとると、
そのｚ増分は、ｄｚ＝２ｙ・ｄｘ＋２ｘ・ｄｙとなる。