




質問<296>2000/8/10
from=文系学部生
「正~角形」
武田先生、先日は私の質問(=指数計算に関する初歩的な質問)に回答
してくださいまして、ありがとうございました。
ところで、また教えていただければ幸いなのですが、
正六角形とは、正三角形を6個くっ付けたものだと思いますが、正12角
形とか、正96角形とかは、2等辺三角形を12個とか96個くっ付けたものな
のでしょうか?
といいますのも、ある数学の雑学の本に、歴史的な円周の計算方法の導
出過程が載っていたのですが、円の中に正六角形を描いて、それをどん
どん細かくしていって、円周を計算したといった事が書かれていたのですが、正12角形とか正96角形というのがどういうものかわからなかった
ので、教えていただければと思いまして。
お返事2000/8/10
from=武田
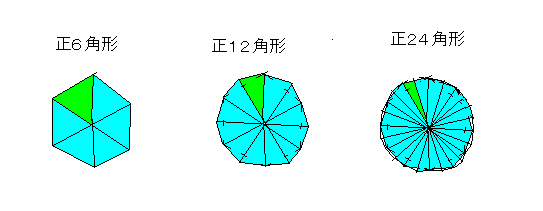 正6角形は、正3角形が6個中に入っている。
正12角形は、2等辺三角形が12個中に入っている。
正24角形は、2等辺三角形が24個中に入っている。
それぞれの緑色の三角形の中心の周りの角は
正6角形のときは、60°(360°÷6=60°)
正12角形のときは、30°(360°÷12=30)
正24角形のときは、15°
正48角形のときは、7.5°
正96角形のときは、3.75°
半径1の円周の長さは、 2πr=6.283185307……
正6角形の6辺の長さの和は、 6×1=6
正12角形は、余弦定理より、12×L=6.211657082……
正24角形 〃 24×L=6.265257227……
正48角形 〃 48×L=6.278700406……
正96角形 〃 96×L=6.282063902……
したがって、
ほぼ正96角形となると、円周の長さと等しくなるのに、昔の人は注目
したのであろう。
正6角形は、正3角形が6個中に入っている。
正12角形は、2等辺三角形が12個中に入っている。
正24角形は、2等辺三角形が24個中に入っている。
それぞれの緑色の三角形の中心の周りの角は
正6角形のときは、60°(360°÷6=60°)
正12角形のときは、30°(360°÷12=30)
正24角形のときは、15°
正48角形のときは、7.5°
正96角形のときは、3.75°
半径1の円周の長さは、 2πr=6.283185307……
正6角形の6辺の長さの和は、 6×1=6
正12角形は、余弦定理より、12×L=6.211657082……
正24角形 〃 24×L=6.265257227……
正48角形 〃 48×L=6.278700406……
正96角形 〃 96×L=6.282063902……
したがって、
ほぼ正96角形となると、円周の長さと等しくなるのに、昔の人は注目
したのであろう。





 正6角形は、正3角形が6個中に入っている。
正12角形は、2等辺三角形が12個中に入っている。
正24角形は、2等辺三角形が24個中に入っている。
それぞれの緑色の三角形の中心の周りの角は
正6角形のときは、60°(360°÷6=60°)
正12角形のときは、30°(360°÷12=30)
正24角形のときは、15°
正48角形のときは、7.5°
正96角形のときは、3.75°
半径1の円周の長さは、 2πr=6.283185307……
正6角形の6辺の長さの和は、 6×1=6
正12角形は、余弦定理より、12×L=6.211657082……
正24角形 〃 24×L=6.265257227……
正48角形 〃 48×L=6.278700406……
正96角形 〃 96×L=6.282063902……
したがって、
ほぼ正96角形となると、円周の長さと等しくなるのに、昔の人は注目
したのであろう。
正6角形は、正3角形が6個中に入っている。
正12角形は、2等辺三角形が12個中に入っている。
正24角形は、2等辺三角形が24個中に入っている。
それぞれの緑色の三角形の中心の周りの角は
正6角形のときは、60°(360°÷6=60°)
正12角形のときは、30°(360°÷12=30)
正24角形のときは、15°
正48角形のときは、7.5°
正96角形のときは、3.75°
半径1の円周の長さは、 2πr=6.283185307……
正6角形の6辺の長さの和は、 6×1=6
正12角形は、余弦定理より、12×L=6.211657082……
正24角形 〃 24×L=6.265257227……
正48角形 〃 48×L=6.278700406……
正96角形 〃 96×L=6.282063902……
したがって、
ほぼ正96角形となると、円周の長さと等しくなるのに、昔の人は注目
したのであろう。




